题目列表(包括答案和解析)
（8分）．如图所示，在空间中取直角坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，场强大小为E。初速度可以忽略的电子经过另一个电势差为U的电场加速后，从y轴上的A点以平行于x轴的方向射入第一象限区域，A点坐标为（0，h）。已知电子的电量为e，质量为m，加速电场的电势差U＞
，电子的重力忽略不计，求：（1）电子从A点进入电场到离开该电场区域所经历的时间t和离开电场区域时的速度v； （2）电子经过x轴时离坐标原点O的距离L。
A、若v0＞
| ||||||
B、v0=
| ||||||
C、若
| ||||||
D、若v0=
|
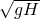，小球b在上升过程中与a球相遇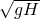； ，小球b在下落过程中肯定与a球相遇；
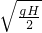，小球b和a不会在空中相遇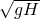；，两球在空中相遇时b球速度为零．
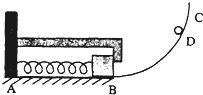如图所示．ABC为光滑轨道，其中AB段水平放置，BC段为半径R的圆弧，AB与BC相切于B点．A处有一竖直墙面，一轻弹簧的一端固定于墙上，另一端与一质量为M的物块相连接．当弹簧处于原长状态时．物块恰能与固定在墙上的L形挡板相接触于B处但无挤压．现使一质量为m，的小球从圆弧轨道上距水平轨道高h处的D点由静止开始下滑．小球与物块相碰后立即共速但不粘连．物块与L形挡板相碰后速度立即减为零也不粘连．（整个过程中．弹簧没有超过弹性限度，小球与L型挡板不接触．不计空气阻力，重力加速度为g）
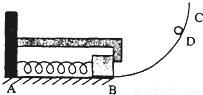如图所示．ABC为光滑轨道，其中AB段水平放置，BC段为半径R的圆弧，AB与BC相切于B点．A处有一竖直墙面，一轻弹簧的一端固定于墙上，另一端与一质量为M的物块相连接．当弹簧处于原长状态时．物块恰能与固定在墙上的L形挡板相接触于B处但无挤压．现使一质量为m，的小球从圆弧轨道上距水平轨道高h处的D点由静止开始下滑．小球与物块相碰后立即共速但不粘连．物块与L形挡板相碰后速度立即减为零也不粘连．（整个过程中．弹簧没有超过弹性限度，小球与L型挡板不接触．不计空气阻力，重力加速度为g）
一、不定项选择题：（本大题共10小题，每小题3分，共30分．全部选对得3分，部分选对得1分，选错或不答得0分）
1
2
3
4
5
6
7
8
9
10
C
AC
C
D
ABC
ACD
CD
ACD
BC
BD
二、填空、实验题：(本大题共4小题，共36分)
11．(6分) 
1.0
12．(12分)（1）甲 （2）BC (3)2.0 1.50 1.0 (6分)
|
14．（6分）（1）2.0
（1分）
（1分） 
（1分）
（1分）
（2分）
（2分）
（2分）
（2分） 
（2分）
（2分）
= 
(2分)
(1分)
高度为
（2分）
（1分）
（1分）
（1分）
（1分）
（1分）
（2分）