
题目列表(包括答案和解析)
已知:点P(a+1,a-1)关于x轴的对称点在反比例函数y= -![]() (x>0)的图像上,y关于x的函数y=k2x2-(2k+1)x+1的图像与坐标轴只有两个不同的交点A﹑B,求P点坐标和△PAB的面积。
(x>0)的图像上,y关于x的函数y=k2x2-(2k+1)x+1的图像与坐标轴只有两个不同的交点A﹑B,求P点坐标和△PAB的面积。

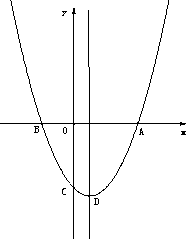
如图,抛物线![]() 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
(1)求抛物线的解析式;
(2)用直尺和圆规作出△ABC的外接圆⊙M,(不写作法,保留作图痕迹),并求⊙M的圆心M的坐标;
(3)将直线AC绕A点顺时针旋转67.5°后交y轴于点P,若抛物线上的点Q关于直线AP对称的点正好落在x轴上,求Q的坐标。
 |
对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得∠APB=60°,则称P为⊙C 的关联点。已知点D( ,
, ),E(0,-2),F(
),E(0,-2),F( ,0)
,0)

(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的关联点是 ;
②过点F作直线交y轴正半轴于点G,使∠GFO=30°,若直线上的点P(m,n)是⊙O的关联点,求m的取值范围;
(2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径r的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com