
题目列表(包括答案和解析)
| ||
| 2 |
| AB |
| BC |
| ||
| 2 |
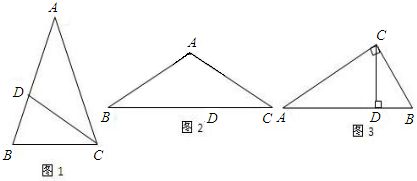
| 1 |
| 2 |
| ||
| 2 |
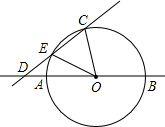 P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.
P,简要说明画出点P的方法(不要求证明);若不存在,说明理由. AB,OD=2.
AB,OD=2. .
.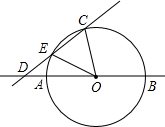 P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.
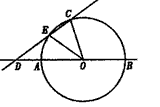
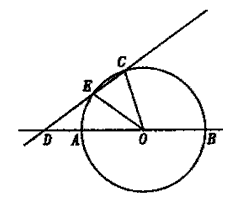
P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.如图,AB是⊙O的直径,点C在⊙O上,∠BOC=108°,过点C作直线CD分别交直线AB和⊙O于点D、E,连接OE,DE=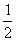 AB,OD=2 。 AB,OD=2 。(1)求∠CDB的度数; (2)我们把有一个内角等于36°的等腰三角形称为黄金三角形。它的腰长与底边长的比(或者底边长与腰长的比)等于黄金分割比 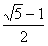 。 。 ①写出图中所有的黄金三角形,选一个说明理由; ②求弦CE的长; ③在直线AB或CD上是否存在点P(点C、D除外),使△POE是黄金三角形?若存在,画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由 |
 |
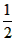 AB,OD=2。
AB,OD=2。 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com