
题目列表(包括答案和解析)
已知:如图,∠ACB=90º,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC于E点,EF⊥AB于F点,
连OE交DC于P,则下列结论:其中正确的有 .
①BC=2DE; ②OE∥AB; ③DE=![]() PD; ④AC•DF=DE•CD.
PD; ④AC•DF=DE•CD.
A.①②③ B.①③④ C.①②④ D.①②③④
 |
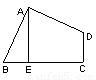
如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
1.当AD=3时,求DE的长;
2.当点E、F在边AC、BC上移动时,设![]() ,
,![]() ,
,
求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
3.在点E、F移动过程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.

如图,四边形ABCD中,∠BAD=∠C=90º,AB=AD,AE⊥BC于E,若线段AE=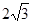 ,则S四边形ABCD= 。
,则S四边形ABCD= 。
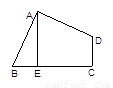
如图,四边形ABCD中,∠BAD=∠C=90º,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD= 。
已知:如图,DG⊥BC ,AC⊥BC,EF⊥AB,∠1="∠2" 求证:CD⊥AB
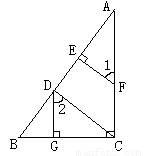
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90º(垂直定义)
∴DG∥AC(_______________________________)
∴∠2=____(_______________________________)
∵∠1=∠2(已知)
∴∠1=∠_____ (等量代换)
∴EF∥CD(_______________________________)
∴∠AEF="∠______" (_______________________________)
∵EF⊥AB (已知)
∴∠AEF=90º (___________________________________ )
∴∠ADC=90º (_______________________________)
∴CD⊥AB (_______________________________)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com