
题目列表(包括答案和解析)
| 3 |
| 2 |
| 1 |
| bn-1 |
|
 ,t≠0,n≥2)
,t≠0,n≥2)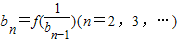 ,求bn;
,求bn; ,那么是否存在实数t,使得数列{(-1)ncn+cn+1}中的每一项都大于1?若存在,求出t的范围;若不存在,请说明理由.
,那么是否存在实数t,使得数列{(-1)ncn+cn+1}中的每一项都大于1?若存在,求出t的范围;若不存在,请说明理由.数列{an}满足an=2an-1+2n+1(n∈N,n≥2),a3=27.
(1)求a1,a2的值;
(2)是否存在一个实数t,使得bn=![]() (an+t)(n∈N+),且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(an+t)(n∈N+),且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列{an}的前n项和Sn.
数列{an}满足an=2an-1+2n+1(n∈N,n≥2),a3=27.
(1)求a1,a2的值;
(2)是否存在一个实数t,使得![]() ,且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
,且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列{an}的前n项和Sn.
数列{an}满足an=2an-1+2n+1(n∈N,n≥2),a3=27.
(1)求a1,a2的值;
(2)是否存在一个实数t,使得![]() ,且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
,且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列{an}的前n项和Sn.
|