
4.如图所示,数轴上点A所表示的数为a,则a的值是 (
 )
)
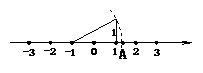 A.
A.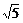 B.
B.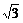 C.
C.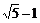
 D.
D.
3.下列各组数据,能作为直角三角形三边长的是 ( )
A.11,15,13 B.1,4,5 C.8,15,17 D.4,5,6
2.下列实数3.14,,π,,0.121121112…,中,有理数有( )个.
A. 1 B. 2 C. 3 D. 4
一、选择题
1.下列QQ的“表情图”中,属于轴对称图形的是( )
A.
 B.
B. C.
C. D.
D.
25.(本小题满分14)
如图7,梯形 中,
中,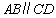 ,
,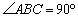 ,
,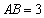 ,
,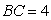 ,
,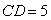 ,点
,点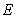 为线段
为线段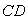 上一动点(不与点
上一动点(不与点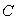 重合),
重合), 关于
关于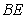 的轴对称图形为
的轴对称图形为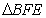 ,连接
,连接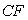 ,设
,设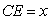 ,
,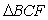
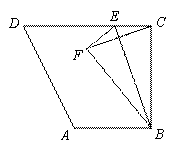 的面积为
的面积为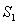 ,
,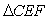 的面积为
的面积为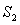 .
.
(1)当点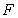 落在梯形
落在梯形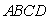 的中位线上时,求
的中位线上时,求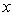 的值;
的值;
(2)试用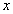 表示
表示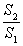 ,并写出
,并写出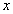 的取值范围;
的取值范围;
(3)当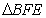 的外接圆与
的外接圆与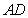 相切时,求
相切时,求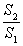 的值.
的值.
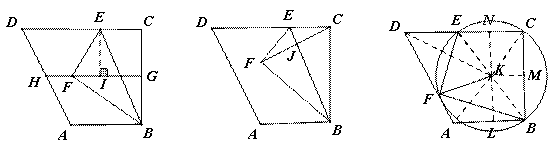
[答案]解:(1)如图1,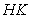 为梯形
为梯形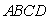 的中位线,则
的中位线,则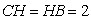 ,过点
,过点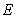 作
作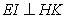 于点
于点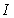 ,则有:
,则有: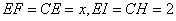
在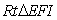 中,有
中,有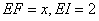
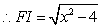
在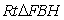 中,
中,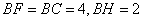
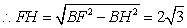
又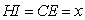
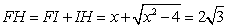
解得: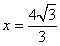
(2)如图2,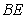 交
交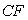 于点
于点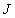 ,
,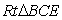 与
与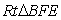 关于
关于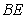 对称,
对称,
则有: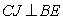 ,
,
又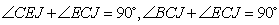
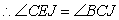
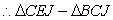
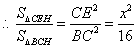
又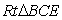 与
与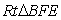 关于
关于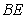 对称,
对称,
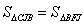
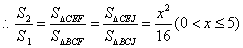
(3)如图3,当
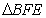 的外接圆与
的外接圆与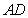 相切时,则
相切时,则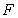 为切点.
为切点.
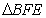 的圆心落在
的圆心落在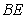 的中点,设为
的中点,设为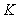
则有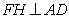 ,过点
,过点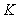 作
作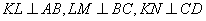 ,
,
连接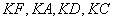 ,得
,得 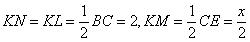
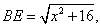 则
则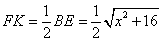
又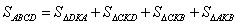
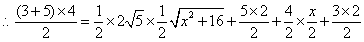
解得: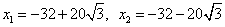 (舍去)
(舍去)
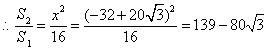
① ② ③
24.(本小题满分14分)
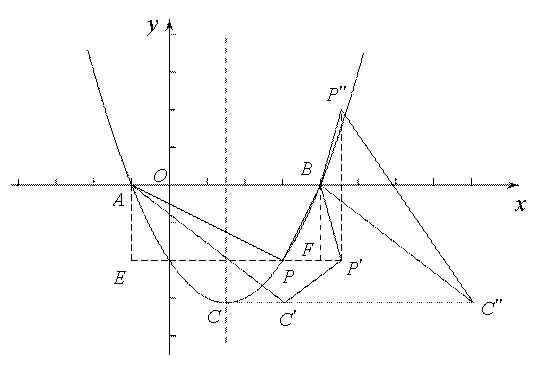
已知平面直角坐标系中两定点A(-1,0),B(4,0),抛物线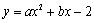 (
( )过点A、B,顶点为C.点P(m,n)(n<0)为抛物线上一点.
)过点A、B,顶点为C.点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式与顶点C的坐标.
(2)当∠APB为钝角时,求m的取值范围.
(3)若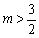 ,当∠APB为直角时,将该抛物线向左或向右平移t(
,当∠APB为直角时,将该抛物线向左或向右平移t(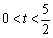 )个单位,点P、C移动后对应的点分别记为
)个单位,点P、C移动后对应的点分别记为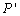 、
、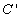 ,是否存在t,使得首尾依次连接A、B、
,是否存在t,使得首尾依次连接A、B、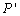 、
、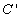 所构成的多边形的周长最短?若存在,求t值并说明抛物线平移的方向;若不存在,请说明理由.
所构成的多边形的周长最短?若存在,求t值并说明抛物线平移的方向;若不存在,请说明理由.
[考点]动点问题.(1)二次函数待定系数法;
(2)存在性问题,相似三角形;
(3)最终问题,轴对称,两点之间线段最短
[答案](1)解:依题意把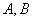 的坐标代入得:
的坐标代入得: 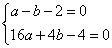 ;解得:
;解得: 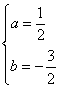
 抛物线解析式为
抛物线解析式为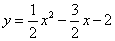
 顶点横坐标
顶点横坐标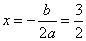 ,将
,将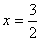 代入抛物线得
代入抛物线得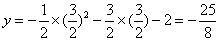
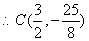
(2)如图,当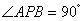 时,设
时,设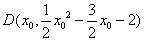 ,
,
则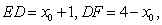
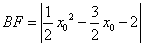
过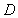 作直线
作直线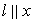 轴,
轴, 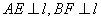
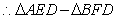
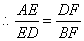
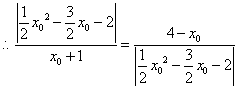 (注意用整体代入法)
(注意用整体代入法)
解得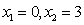
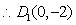 ,
,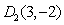
当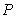 在
在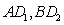 之间时,
之间时,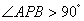
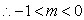 或
或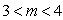 时,
时,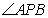 为钝角.
为钝角.
(3)依题意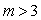 ,且
,且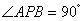
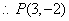
设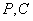 移动
移动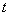 (
(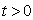 向右,
向右,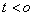 向左)
向左)
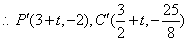
连接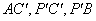
则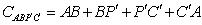
又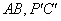 的长度不变
的长度不变
 四边形周长最小,只需
四边形周长最小,只需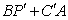 最小即可
最小即可
将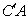 沿
沿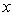 轴向右平移5各单位到
轴向右平移5各单位到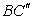 处
处
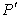 沿
沿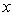 轴对称为
轴对称为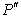
∴当且仅当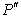 、B、
、B、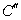 三点共线时,
三点共线时,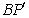
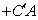 最小,且最小为
最小,且最小为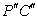 ,此时
,此时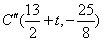
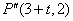 ,设过
,设过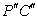 的直线为
的直线为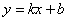 ,代入
,代入 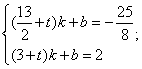
∴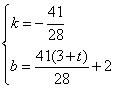 即
即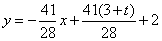
将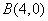 代入,得:
代入,得: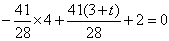 ,解得:
,解得: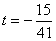
∴当,P、C向左移动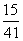 单位时,此时四边形ABP’C’周长最小。
单位时,此时四边形ABP’C’周长最小。
23、(本小题满分12分)
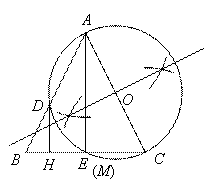
如图6, 中,
中,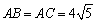 ,
,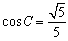 .
.
(1)动手操作:利用尺规作以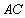 为直径的
为直径的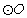 ,并标出
,并标出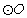 与
与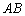 的交点
的交点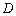 ,与
,与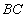 的交点
的交点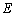
(保留作图痕迹,不写作法):
(2)综合应用:在你所作的圆中,
①求证: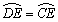 ;
;
②求点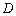 到
到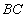 的距离.
的距离.
[考点](1)尺规作图;(2)①圆周角、圆心角定理; ②勾股定理,等面积法
[分析](1)先做出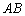 中点
中点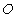 ,再以
,再以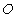 为圆心,
为圆心,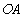 为半径画圆.
为半径画圆.
(2)①要求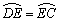 ,根据圆心角定理,同圆中圆心角相等所对的弧也相等,只需证出
,根据圆心角定理,同圆中圆心角相等所对的弧也相等,只需证出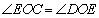 即可,再根据等腰三角形中的边角关系转化.
即可,再根据等腰三角形中的边角关系转化.
②首先根据已知条件可求出 ,依题意作出高
,依题意作出高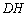 ,求高则用勾股定理或面积法,注意到
,求高则用勾股定理或面积法,注意到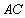 为直径,所以想到连接
为直径,所以想到连接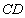 ,构造直角三角形,进而用勾股定理可求出
,构造直角三角形,进而用勾股定理可求出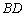 ,
,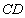 的长度,那么在
的长度,那么在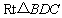 中,求其高,就只需用面积法即可求出高
中,求其高,就只需用面积法即可求出高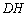 .
.
[答案](1)如图所示,圆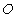 为所求
为所求
(2)①如图连接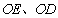 ,设
,设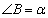 ,
,
又
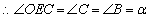
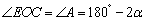
则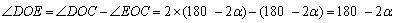
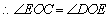
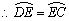
②连接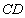 ,过
,过 作
作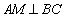 于
于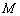 ,过
,过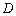 作
作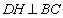 于
于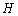
 cosC=
cosC=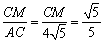 ,
又
,
又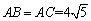
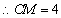 ,
,
又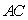 为直径
为直径
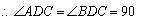
设 ,则
,则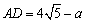 ,
,
在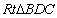 和
和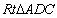 中,
中,
有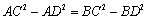
即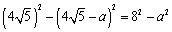
解得:
即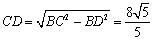
又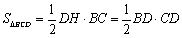
即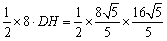
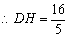
22、(本小题满分12分)
从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
[考点]行程问题的应用
[分析]路程=速度×时间,分式方程的实际应用考察
[解析]
(1)依题意可得,普通列车的行驶路程为400×1.3=520(千米)
(2)设普通列车的平均速度为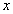 千米/时,则高铁平均速度为
千米/时,则高铁平均速度为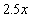 千米/时.
千米/时.
依题意有: 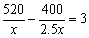 可得:
可得: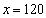
答:高铁平均速度为 2.5×120=300千米/时.
21.(本小题满分12分)
已知一次函数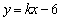 的图像与反比例函数
的图像与反比例函数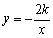 的图像交于
的图像交于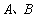 两点,点
两点,点 的横坐标为2.
的横坐标为2.
(1)求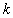 的值和点
的值和点 的坐标;
的坐标;
(2)判断点 的象限,并说明理由.
的象限,并说明理由.
[考点]1一次函数;2反比例函数;3函数图象求交点坐标
[分析]第(1)问根据 点是两个图象的交点,将
点是两个图象的交点,将 代入联立之后的方程可求出
代入联立之后的方程可求出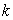 ,再将
,再将 点的横坐标代入函数表达式求出纵坐标;第(2)问根据一次函数与反比例函数的解析式分析两图像经过的象限,得出两图像交点所在象限.此题主要考查反比例函数与一次函数的性质
点的横坐标代入函数表达式求出纵坐标;第(2)问根据一次函数与反比例函数的解析式分析两图像经过的象限,得出两图像交点所在象限.此题主要考查反比例函数与一次函数的性质
[答案]解:(1)将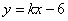 与
与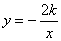 联立得:
联立得:
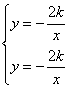
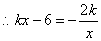 1
1
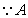 点是两个函数图象交点,将
点是两个函数图象交点,将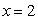 带入1式得:
带入1式得:
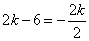 解得
解得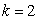
故一次函数解析式为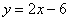 ,反比例函数解析式为
,反比例函数解析式为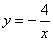
将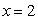 代入
代入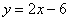 得,
得,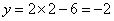
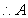 的坐标为
的坐标为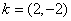
(2)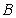 点在第四象限,理由如下:
点在第四象限,理由如下:
一次函数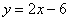 经过第一、三、四象限,反比例函数经过第二、四象限,
经过第一、三、四象限,反比例函数经过第二、四象限,
因此它们的交点都是在第四象限.
20.(本小题满分10分)
某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
|
自选项目 |
人数 |
频率 |
|
立定跳远 |
9 |
0.18 |
|
三级蛙跳 |
12 |
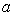 |
|
一分钟跳绳 |
8 |
0.16 |
|
投掷实心球 |
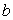 |
0.32 |
|
推铅球 |
5 |
0.10 |
|
合计 |
50 |
1 |
(1)求 ,
,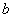 的值;
的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.
[考点](1)频率(2)①频率与圆心角; ②树状图,概率
[分析](1)各项人数之和等于总人数50 ; 各项频率之和为1(2)所占圆心角=频率*360
(3)画出列表图,至多有一名女生包括有一个女生和一个女生都没有两种情况.
[答案](1)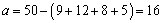
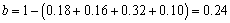
(2)“一分钟跳绳”所占圆心角=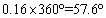
(3)至多有一名女生包括两种情况有1个或者0个女生
列表图:
|
|
男A |
男B |
男C |
女D |
女E |
|
男A |
|
(A,B) |
(A,C) |
(A,D) |
(A,E) |
|
男B |
(B,A) |
|
(B,C) |
(B,D) |
(B,E) |
|
男C |
(C,A) |
(C,B) |
|
(C,D) |
(C,E) |
|
女D |
(D,A) |
(D,B) |
(D,C) |
|
(D,E) |
|
女E |
(E,A) |
(E,B) |
(E,C) |
(E,D) |
|
有1个女生的情况:12种
有0个女生的情况:6种
至多有一名女生包括两种情况18种
至多有一名女生包括两种情况=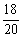 =
=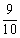 =0.90
=0.90
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com