
18.(13分)
解:(1)分别令n=1,2,3得
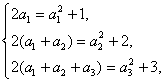
∵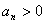 ,∴
,∴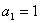 ,
,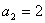 ,
,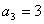 .…………………………………………………3分
.…………………………………………………3分
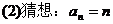 ……………………………………………………………………………4分
……………………………………………………………………………4分
下面用数学归纳法证明:
(1)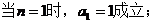 ……………………………………………………………5分
……………………………………………………………5分
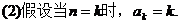 ………………………………………………………………6分
………………………………………………………………6分
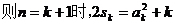
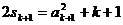
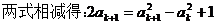 ………………………………………………………8分
………………………………………………………8分
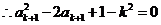
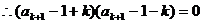 …………………………………………………………10分
…………………………………………………………10分
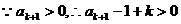
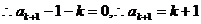 …………………………………………………………11分
…………………………………………………………11分
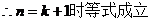 ……………………………………………………………………12分
……………………………………………………………………12分
由(1)(2)可得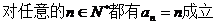 ……………………………………13分
……………………………………13分
17.(13分)
解(1)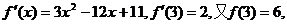
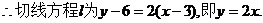 ………………………………………………6分
………………………………………………6分
(2)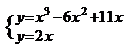
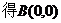 ……………………………………………………10分
……………………………………………………10分
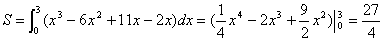 …………………………13分
…………………………13分
三、解答题
16.(13分)
解:(1)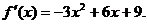 ………………………………………………………2分
………………………………………………………2分  ………………4分
………………4分
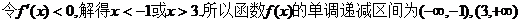 ………………………………………………………………………………………………………6分
………………………………………………………………………………………………………6分
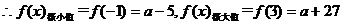 …………………………………8分
…………………………………8分
(2)由(1)知若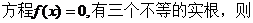
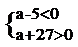 …………………………………………………………………………………11分
…………………………………………………………………………………11分
解得-27<a<5 …………………………………………………………………………………12分
所以a 的取值范围是(-27,5)………………………………………………………………13分
15.设切点坐标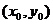 ,由题意得
,由题意得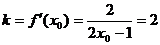

二、填空题
11.3
12.1 13.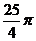 14.< 15.
14.< 15.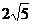
提示:14.假设M<N,则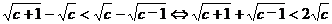
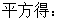
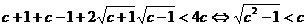
再平方得: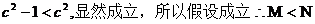
10.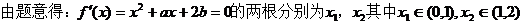 则
则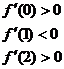
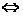
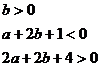 然后用线性规划解出答案
然后用线性规划解出答案
一、选择题
1.B 2.C 3.B 4.D 5.A 6.B 7.B 8.B 9.D 10.C
提示:9.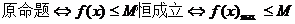
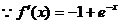
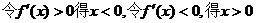
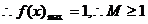
21.(本小题满分12分)
给出定义在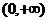 上的三个函数:
上的三个函数: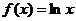 ,
,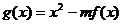
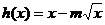 ,已知
,已知 在
在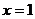 处取极值.
处取极值.
(1)求 的值及函数
的值及函数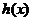 的单调区间;
的单调区间;
(2)求证:当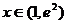 时,恒有
时,恒有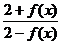 >
>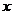 成立.
成立.
重庆开县实验中学2014级高二下期末训练(一)答案
20.(本小题满分12分)
已知函数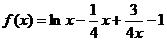 .
.
(1)求函数 在
在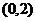 上的最小值;
上的最小值;
(2)设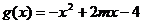 ,若对任意
,若对任意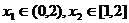 ,不等式
,不等式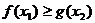 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
19.(本小题满分12分)
已知函数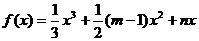 (
( 、
、 为常数).
为常数).
(1)若 在
在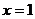 和
和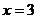 处取得极值,试求
处取得极值,试求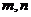 的值;
的值;
(2)若 在
在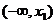 、
、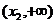 上单调递增,且在
上单调递增,且在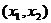 上单调递减,又满足
上单调递减,又满足
 >1.求证:
>1.求证: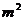 >
>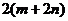 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com