
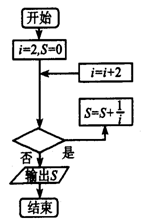
7、如图给出的是计算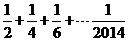 的值的程序框图,其中判断框内应填入的是( )
的值的程序框图,其中判断框内应填入的是( )
 A.
A.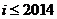 B.
B.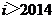 C.
C.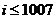 D.
D.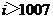
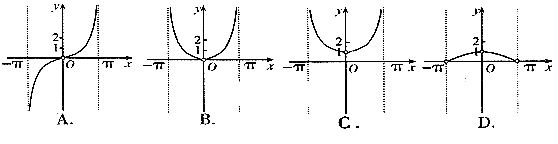
6. 函数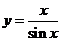 ,
,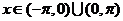 的图象可能是下列图象中的 ( )
的图象可能是下列图象中的 ( )
5.在面积为S的△ABC内任投一点P,则△PBC的面积大于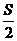 的概率是( )
的概率是( )
A.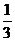 B.
B.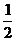 C.
C.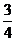 D.
D.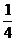
4、定义在R上的函数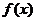 既是偶函数又是周期函数.若
既是偶函数又是周期函数.若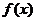 的最小正周期是
的最小正周期是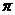 ,且当
,且当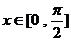 时,
时,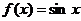 ,则
,则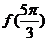 的值为 ( )
的值为 ( )
A. 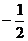 B.
B. 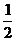 C.
C. 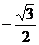 D.
D. 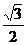
3.某班级共有学生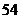 人,现根据学生的学号,用系统抽样的方法,抽取一个容量为
人,现根据学生的学号,用系统抽样的方法,抽取一个容量为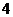 的样本.已知
的样本.已知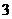 号,
号,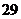 号,
号,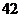 号同学在样本中,那么样本中还有一个同学的学号是( )
号同学在样本中,那么样本中还有一个同学的学号是( )
A.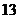 B.
B.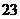 C.
C.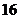 D.
D.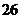
2.一个单位有职工160人,其中有业务员104人,管理人员32人,后勤服务人员24人,要从中
抽取一个容量为20的 样本,用分层抽样的方法抽取样本,则在20人的样本中应抽取管理人员人数
样本,用分层抽样的方法抽取样本,则在20人的样本中应抽取管理人员人数
为 ( ) A. 3 B. 4 C. 5 D. 6
一、选择题
1、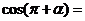
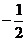 ,
,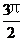 <α<
<α<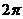 ,
, 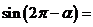 ( )
( )
A. 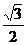 B.
B. 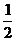 C.
C.
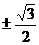 D.
D. 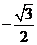
22. (本小题满分12分)
已知抛物线C: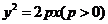 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且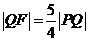 .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线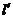 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
解:(1)设Q(x0,4),代入由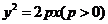 中得x0=
中得x0=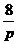 ,
,
所以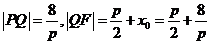 ,由题设得
,由题设得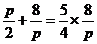 ,解得p=-2(舍去)或p=2.
,解得p=-2(舍去)或p=2.
所以C的方程为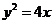 .
.
(2)依题意知直线l与坐标轴不垂直,故可设直线l的方程为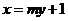 ,(m≠0)代入
,(m≠0)代入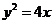 中得
中得
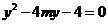 ,
,
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4,
故AB的中点为D(2m2+1,2m),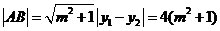 ,
,
有直线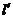 的斜率为-m,所以直线
的斜率为-m,所以直线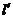 的方程为
的方程为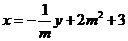 ,将上式代入
,将上式代入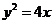 中,并整理得
中,并整理得
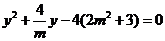 .
.
设M(x3,y3),N(x4,y4),则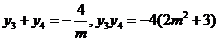 .
.
故MN的中点为E(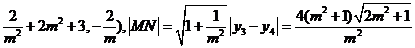 ).
).
由于MN垂直平分AB,故A,M,B,N四点在同一个圆上等价于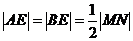 ,从而
,从而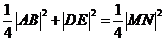 ,即
,即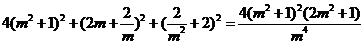 ,化简得
,化简得
m2-1=0,解得m=1或m=-1,
所以所求直线l的方程为x-y-1=0或x+y-1=0.
21. (本小题满分12分)函数f(x)=ax3+3x2+3x(a≠0).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(1,2)是增函数,求a的取值范围.
解:(1)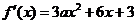 ,
,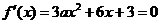 的判别式△=36(1-a).
的判别式△=36(1-a).
(i)若a≥1,则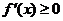 ,且
,且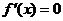 当且仅当a=1,x=-1,故此时f(x)在R上是增函数.
当且仅当a=1,x=-1,故此时f(x)在R上是增函数.
(ii)由于a≠0,故当a<1时,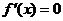 有两个根:
有两个根: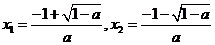 ,
,
若0<a<1,则当x∈(-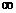 ,x2)或x∈(x1,+
,x2)或x∈(x1,+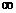 )时,
)时,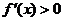 ,故f(x)在(-
,故f(x)在(-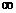 ,x2),(x1,+
,x2),(x1,+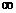 )上是增函数;
)上是增函数;
当x∈(x2,x1)时,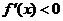 ,故f(x)在(x2,x1)上是减函数;
,故f(x)在(x2,x1)上是减函数;
(2)当a>0,x>0时, 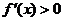 ,所以当a>0时,f(x)在区间(1,2)是增函数.
,所以当a>0时,f(x)在区间(1,2)是增函数.
若a<0时,f(x)在区间(1,2)是增函数当且仅当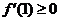 且
且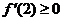 ,解得
,解得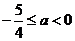 .
.
综上,a的取值范围是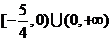 .
.
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分10分)
数列{an}满足a1=1,a2=2,an+2=2an+1-an+2.
(1)设bn=an+1-an,证明{bn}是等差数列;
(2)求数列{an}的通项公式.
解:(1)由an+2=2an+1-an+2得an+2- an+1=an+1-an+2,即bn+1=bn+2,又b1=a2-a1=1.
所以{bn}是首项为1,公差为2的等差数列;
(2) 由(1)得bn=1+2(n-1),即an+1-an=2n-1.于是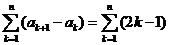
于是an-a1=n2-2n,即an=n2-2n +1+a1.又a1=1,所以{an}的通项公式为an=n2-2n +2.
(18)(本小题满分10分)
△ABC的内角A,B,C的对边分别是a,b,c,已知3acosC=2ccosA,tanA=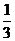 ,求B.
,求B.
解:由题设和正弦定理得,3sinAcosC=2sinCcosA,
所以3tanAcosC=2sinC.
因为tanA=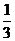 ,所以cosC=2sinC.
,所以cosC=2sinC.
tanC=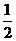 .
.
所以tanB=tan[180 -(A+C)]
-(A+C)]
=-tan(a+c)
=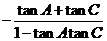 =-1,
=-1,
即B=135 .
.
(19)(本小题满分12分)
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为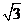 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.
解法一:(1)∵A1D⊥平面ABC, A1D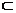 平面AA1C1C,故平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,连结A1C,因为侧面AA1C1C是棱形,所以AC1⊥A1C,由三垂线定理的AC1⊥A1B.
平面AA1C1C,故平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,连结A1C,因为侧面AA1C1C是棱形,所以AC1⊥A1C,由三垂线定理的AC1⊥A1B.
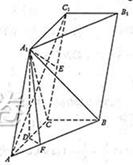
(2) BC⊥平面AA1C1C,BC 平面BCC1B1,故平面AA1C1C⊥平面BCC1B1,
平面BCC1B1,故平面AA1C1C⊥平面BCC1B1,
作A1E⊥C1C,E为垂足,则A1E⊥平面BCC1B1,又直线A A1∥平面BCC1B1,因而A1E为直线A A1与平面BCC1B1间的距离,A1E=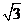 ,因为A1C为∠ACC1的平分线,故A1D=A1E=
,因为A1C为∠ACC1的平分线,故A1D=A1E=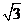 ,
,
作DF⊥AB,F为垂足,连结A1F,由三垂线定理得A1F⊥AB,故∠A1FD为二面角A1-AB-C的平面角,由AD=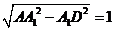 ,得D为AC的中点,DF=
,得D为AC的中点,DF=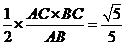 ,tan∠A1FD=
,tan∠A1FD=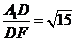 ,所以二面角A1-AB-C的大小为arctan
,所以二面角A1-AB-C的大小为arctan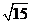 .
.
解法二:以C为坐标原点,射线CA为x轴的正半轴,以CB的长为单位长,建立如图所示的空间直角坐标系C-xyz,由题设知A1D与z轴平行,z轴在平面AA1C1C内.
(1)设A1(a,0,c),由题设有a≤2,A(2,0,0)B(0,1,0),则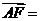 (-2,1,0),
(-2,1,0),
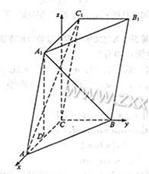
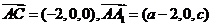 ,
,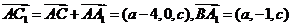 ,由
,由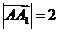 得
得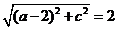 ,即
,即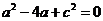 ,于是
,于是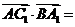
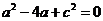 ①,所以
①,所以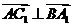 .
.
(2)设平面BCC1B1的法向量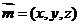 ,则
,则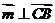 ,
,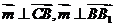 ,即
,即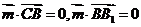 ,因
,因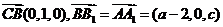 ,故y=0,且(a-2)x-cz=0,令x=c,则z=2-a,
,故y=0,且(a-2)x-cz=0,令x=c,则z=2-a,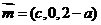 ,点A到平面BCC1B1的距离为
,点A到平面BCC1B1的距离为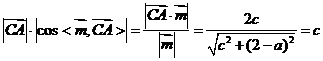 ,又依题设,点A到平面BCC1B1的距离为
,又依题设,点A到平面BCC1B1的距离为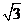 ,所以c=
,所以c= 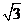 .代入①得a=3(舍去)或a=1.于是
.代入①得a=3(舍去)或a=1.于是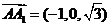 ,
,
设平面ABA1的法向量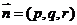 ,则
,则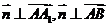 ,即
,即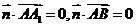 .
.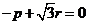 且-2p+q=0,令p=
且-2p+q=0,令p=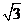 ,则q=2
,则q=2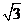 ,r=1,
,r=1,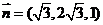 ,又
,又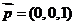 为平面ABC的法向量,故cos
为平面ABC的法向量,故cos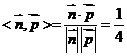 ,所以二面角A1-AB-C的大小为arccos
,所以二面角A1-AB-C的大小为arccos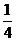
20. (本小题满分12分)
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6, 0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买k台设备供甲、乙、丙、丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.
解:记Ai表示事件:同一工作日乙、丙中恰有i人需使用设备,i=0,1,2.
B表示事件:甲需使用设备.
C表示事件:丁需使用设备.
D表示事件:同一工作日至少3人需使用设备.
E表示事件:同一工作日4人需使用设备.
F表示事件:同一工作日需使用设备的人数大于k.
(1)D=A1·B·C+A2·B+A2·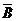 ·C
·C
P(B)=0.6,P(C)=0.4,P(Ai)=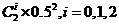 .
.
所以P(D)=P(A1·B·C+A2·B+A2·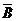 ·C)= P(A1·B·C)+P(A2·B)+P(A2·
·C)= P(A1·B·C)+P(A2·B)+P(A2·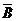 ·C)
·C)
= P(A1P)·P(B)·P(C)+P(A2)·P(B)+P(A2)·p(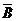 )·p(C)=0.31.
)·p(C)=0.31.
(2)由(1)知,若k=3,则P(F)==0.31>0.1.
又E=B·C·A2,P(E)=P(B·C·A2)= P(B)·P(C)·P(A2)=0.06;
若k=4,则P(F)=0.06<0.1.
所以k的最小值为3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com