
13.[解析]平抛运动水平位移x=v0t (2分)
竖直位移h= gt
gt 2 (2分)
2 (2分)
解以上两式得x=v0·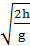 (2分)
(2分)
由重力等于万有引力mg=G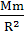 得 (2分)
得 (2分)
g=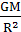 (2分)
(2分)
所以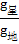 =
=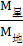 (
(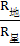 )2=9×
)2=9× =36 (2分)
=36 (2分)
 =
=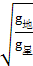 =
=
x星= x地=10m (2分)
x地=10m (2分)
答案:10m
12.[解析]选B。b、c都是地球的卫星,共同遵循地球对它们的万有引力提供向心力,是可以比较的。a、c是在同一平面内以相同角速度转动的,也是可以比较的。在某时刻c在a的正上方,则以后永远在a的正上方。对b有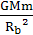 =m(
=m(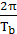 )2Rb, GM=gR2,化简得Tb=2π
)2Rb, GM=gR2,化简得Tb=2π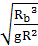 =2×
=2×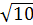 ×
×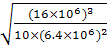 s=2×104s,在48h内b转动的圈数为n=
s=2×104s,在48h内b转动的圈数为n=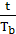 =
=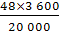 =8.64,所以B正确。
=8.64,所以B正确。
[总结提升]天体问题的两步求解法
(1)建立一个模型:天体绕中心天体做匀速圆周运动,万有引力提供向心力,即:
F万=F向。
(2)写出两组式子:
a.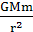 =m
=m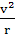 =mω2r=m(
=mω2r=m(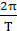 )2r=ma;
)2r=ma;
b.代换关系:天体表面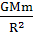 =mg0,空间轨道上
=mg0,空间轨道上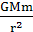 =ma。
=ma。
11.[解析]选B。设两颗星的质量分别为m1、m2,做圆周运动的半径分别为r1、r2,根据万有引力提供向心力可得:G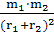 =m1r1
=m1r1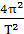 ,G
,G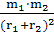 =m2r2
=m2r2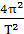 ,联立解得:m1+m2=
,联立解得:m1+m2=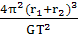 ,即T2=
,即T2=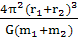 ,因此,当两星总质量变为原来的k倍,两星之间的距离变为原来的n倍时,两星圆周运动的周期为T′=
,因此,当两星总质量变为原来的k倍,两星之间的距离变为原来的n倍时,两星圆周运动的周期为T′=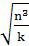 T,选项B正确,其他选项均错。
T,选项B正确,其他选项均错。
10.[解题指南]解答本题时可按以下思路分析:

[解析]选B。“天宫一号”绕地球做匀速圆周运动,向心力由万有引力提供。设地球质量为M,“天宫一号”质量为m,则变轨前:G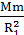 =m
=m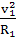 ,变轨后:G
,变轨后:G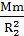 =m
=m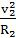 ,联立以上两式解得:
,联立以上两式解得: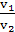 =
=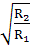 ,故选项B正确。
,故选项B正确。
9.[解析]选C。根据图像可得物体下落25m,用的总时间为2.5s,根据自由落体公式可求得行星表面的重力加速度,C项正确;根据行星表面的万有引力约等于重力,只能求出行星质量与行星半径平方的比值,不能求出行星的质量和半径,A项和B项错误;因为物体质量未知,不能确定物体受到行星的引力大小,D项错误。
8.[解析]选A、B。由G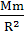 =mg得g=G
=mg得g=G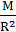 ,计算得火星表面的重力加速度约为地球表面的
,计算得火星表面的重力加速度约为地球表面的 ,A正确;由
,A正确;由 G
G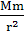 =m(
=m(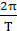 )2r得T=2π
)2r得T=2π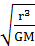 ,公转轨道半径大的周期长,B正确;周期长的线速度小(或由v=
,公转轨道半径大的周期长,B正确;周期长的线速度小(或由v=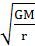 ,判断轨道半径大的线速度小),C错;公转向心加速度a=G
,判断轨道半径大的线速度小),C错;公转向心加速度a=G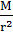 ,判断轨道半径大的向心加速度小,D错。
,判断轨道半径大的向心加速度小,D错。
7.[解析]选B、C。在远距离导引段,“神舟十号”位于“天宫一号”的后下方的低轨道上飞行,通过适当加速,“神舟十号”向高处跃升,并追上“天宫一号” 与之完成对接,A错,B对。“神舟十号”与“天宫一号”组合体在地球上空数百公里的轨道上运动,线速度小于第一宇宙速度7.9km/s,C对。分离后,“天宫一号”上升至较高轨道上运动,线速度变小,D错。
与之完成对接,A错,B对。“神舟十号”与“天宫一号”组合体在地球上空数百公里的轨道上运动,线速度小于第一宇宙速度7.9km/s,C对。分离后,“天宫一号”上升至较高轨道上运动,线速度变小,D错。
6.[解析]选B。研究地球绕太阳做圆周运动的向心力,由太阳对地球的万有引力提供向心力。
根据万有引力定律和牛顿第二定律有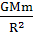 =
=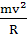 ,整理得M=
,整理得M=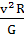
太阳绕银河系运动也是由万有引力提供向心力,
同理可得M′=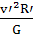 。
。
由题意知v′=7v,R′=2×109R,
解得M′≈1011M,故B正确。
[总结提升]求天体质量和密度的方法
天体的质量或密度的求解问题是近几年考试的热点,这类问题的求解方法归纳如下:
(1)利用某星球表面的重力约等于万有引力来求。若某星球的质量为M,半径为R,其表面的重力加速度为g,则mg=G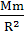 ,故星球的质量M=
,故星球的质量M=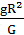 。
。
(2)利用天体(或卫星)做圆周运动的向心力等于万有引力来求,即G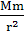 =m
=m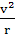 =
=
mω2r=m(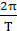 )2r。可求得天体的质量M=
)2r。可求得天体的质量M=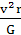 =
=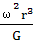 =
=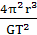 。此法所求的质量为中心天体的质量,实际中轨道半径r和周期T较容易测得,故常用上式中的M=
。此法所求的质量为中心天体的质量,实际中轨道半径r和周期T较容易测得,故常用上式中的M=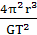 来求天体的质量。
来求天体的质量。
(3)天体的密度ρ= =
=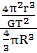 =
=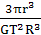 。式中r、R分别为轨道半径和被求天体的半径,两者不可混淆。当卫星做近地绕行时,r≈R,被求天体的密度ρ=
。式中r、R分别为轨道半径和被求天体的半径,两者不可混淆。当卫星做近地绕行时,r≈R,被求天体的密度ρ=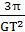 ,此时只要知道周期T,就可求得天体的密度。
,此时只要知道周期T,就可求得天体的密度。
5.[解析]选A、B、C。由黄金代换式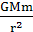 =mg可求出
=mg可求出 月球的质量,代入密度公式可求出月球的密度,由
月球的质量,代入密度公式可求出月球的密度,由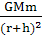 =m
=m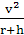 =ma可求出卫星所在处的加速度和卫星的线速度,因为卫星的质量未知,故没法求卫星所需的向心力。
=ma可求出卫星所在处的加速度和卫星的线速度,因为卫星的质量未知,故没法求卫星所需的向心力。
4.[解析]选D。本题考查卫星运行的轨道。同步卫星相对地球静止,自西向东转,所有的卫星都必须以地心为圆心,因此同步卫星在赤道上空,与赤道线是共面同心圆,故D正确。
[变式备选]我国已经成功发射北斗COMPASS—G1地球同步卫星。据了解这已是北斗卫星导航系统发射的第三颗地球同步卫星。则对于这三颗已发射的同步卫星,下列说法中正确的是 ( )
A.它们的运行速度大小相等,且都小于7.9km/s
B.它们的运行周期可能不同
C.它们离地心的距离可能不同
D.它们的向心加速度与静止在赤道上物体的向心加速度大小相等
[解析]选A。同步卫星运动的周期都是24h,由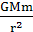 =mr
=mr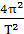 ,可知所有的同步卫星离地面的高度一定,运行的速度都比第一宇宙速度小,故A项正确,B、C项错误;由a=ω2r,静止在赤道上的物体与同步卫星的角速度相同,故同步卫星的向心加速度大,D项错误。
,可知所有的同步卫星离地面的高度一定,运行的速度都比第一宇宙速度小,故A项正确,B、C项错误;由a=ω2r,静止在赤道上的物体与同步卫星的角速度相同,故同步卫星的向心加速度大,D项错误。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com