
6.为建设生态滨州,我市某中学在植树节那天,组织初三年级八个班的学生到西城新区植树,各班植树情况如下表:
|
班级 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
合计 |
|
棵数 |
15 |
18 |
22 |
25 |
29 |
14 |
18 |
19 |
160 |
下列说法错误的是( )
A.这组数据的众数是18
B.这组数据的中位数是18.5
C.这组数据的平均数是20
 D.以平均数20(棵)为标准评价这次植树活动中各班植树任务完成情况比较合理
D.以平均数20(棵)为标准评价这次植树活动中各班植树任务完成情况比较合理
5.不等式组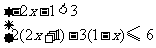 的解集为( )
的解集为( )
A.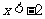 B.
B.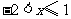 C.
C.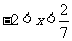 D.
D.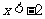 或
或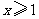
4. 如图1,在半径为10的
如图1,在半径为10的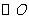 中,如果弦心距
中,如果弦心距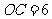 ,
,
那么弦 的长等于( )
的长等于( )
A.4 B.8
C.16 D.32
3.2006年5月20日,三峡大坝全线封顶,标志着世界上最大的水利枢纽工程主体工程基本完工.据报道,三峡水电站年平均发电量为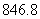 亿度,用科学记数法记作(保留三位有效数字)( )
亿度,用科学记数法记作(保留三位有效数字)( )
A.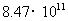 度 B.
度 B.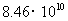 度 C.
度 C.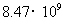 度 D.
度 D.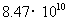 度
度
2.下列运算中,正确的是( )
A.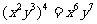 B.
B.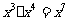
C.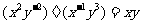 D.
D.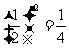
1.函数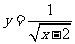 的自变量
的自变量 的取值范围是( )
的取值范围是( )
A.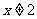 B.
B.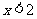 C.
C.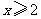 D.
D.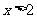
25. 问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题:
① 如图1,在正三角形ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON = 60°,则BM = CN.
②
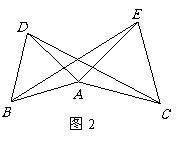
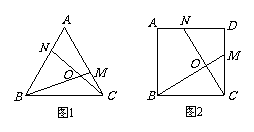 如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON = 90°,则BM = CN.
如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON = 90°,则BM = CN.
然后运用类比的思想提出了如下的命题:
③
 如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON = 108°,则BM = CN.
如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON = 108°,则BM = CN.
任务要求
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对的得4分,选②做对的得3分,选③做对的得5分)
 (2)请你继续完成下面的探索:
(2)请你继续完成下面的探索:
① 如图4,在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,问当∠BON等于多少度时,结论BM = CN成立?(不要求证明)
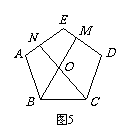
② 如图5,在五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,当∠BON = 108°时,请问结论BM = CN是否还成立?若成立,请给予证明;若不成立,请说明理由.
(1)我选 .
证明:
24. 小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a > 8),就站到A窗口队伍的后面. 过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少(用含a的代数式表示)?
(2)此时,若小杰迅速从A窗口队伍转移到B窗口队伍后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其他因素).
23. 如图,在梯形纸片ABCD中,AD∥BC,AD > CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C’E
(1)求证:四边形CDC’E是菱形;
(2)若BC = CD + AD,试判断四边形ABED的形状,并加以证明.

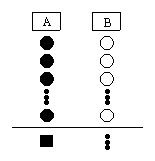
22. 某文具店销售的水笔只有A、B、C三种型号,下面表格和统计图分别给出了上月这三种型号水笔每支的利润和销售量.
某文具店销售的水笔只有A、B、C三种型号,下面表格和统计图分别给出了上月这三种型号水笔每支的利润和销售量.
A、B、C三种水笔销售量统计图
A、B、C三种水笔每支利润统计表
|
水笔型号 |
A |
B |
C |
|
每支利润(元) |
0.6 |
0.5 |
1.2 |
 (1)分别计算该店上月这三种型号水笔的利润,并将利润分布情况用扇形统计图表示;
(1)分别计算该店上月这三种型号水笔的利润,并将利润分布情况用扇形统计图表示;
(2)若该店计划下月共进这三种型号水笔600支,结合上月销售情况,你认为A、B、C三种型号的水笔各进多少支总利润最高?此时所获得的总利润是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com