26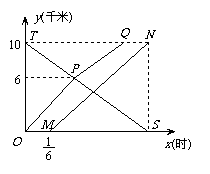．如图，三人在相距10千米的两地练习骑自行车，折线OPQ、线段MN和TS分别表示甲、乙和丙距某地的路程y与时间x之间的函数关系．已知，甲以18千米/时的速度走完6千米后改变速度匀速前进，20分钟到达终点．解答下列问题：

　　 (1)求线段PQ的函数解析式；

　　 (2)求乙和丙从甲出发多少分钟相遇，相遇点

　　　　 距甲出发地多少千米．

www.1230.org 初中数学资源网

单元学习评价四(一次函数)

25．某企业有甲、乙两个长方体的蓄水池，将甲池中的水以每小时6立方米的速度注入乙池，甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示，结合图象回答下列问题：

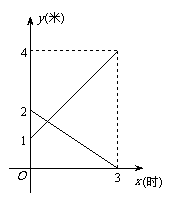　　 (1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式；

　　 (2)求注水多长时间甲、乙两个蓄水池水的深度相同；

　　 (3)求注水多长时间甲、乙两个蓄水池的蓄水量相同．

24．如图，正方形ABCD的边长是4，将此正方形置于平面直角坐标系xOy中，使AB落

在x轴的正半轴上，C、D落在第一象限，经过点C的直线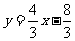交x轴于点E．

(1)求四边形AECD的面积；

(2)在坐标平面内，经过点E的直线能否将正方形ABCD分成面积相等的两部分？

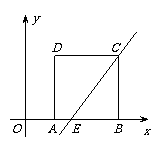若能，求出这条直线的解析式，若不能，说明理由．

www.1230.org 初中数学资源网

23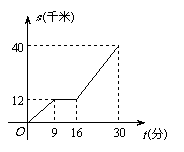．如图所示，是汽车行驶的路程s(千米)与时间t(分)函数关系图．观察图中所提供的信息，解答下列问题：

　　 (1)汽车在前9分钟内的平均速度是多少？

　　 (2)汽车在中途停了多长时间？

　　 (3)当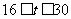时，求s与t的函数解析式．

22．已知，点A(4，)，B(6，)，C(4，n)在同一条直线上．

　　 (1)试求直线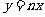的解析式；

　　 (2)在x轴上找一点P，使PA+PB最短，求出满足条件的点P的坐标．

21．某地长途汽车客运公司规定旅客可以随身携带一定重量的行李，如果超出规定，则需购买行李票，行李票费用y(元)是行李重量x(千克)的一次函数，如图所示．求：

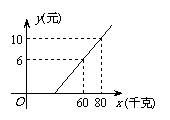　　 (1)y与x之间的函数解析式；

　　 (2)旅客最多可免费携带行李多少千克？

20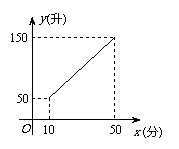．如图所示，是某校一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系．

(1)求y与x的函数关系式；

(2)在(1)的条件下，求在30分钟时水箱有多少升水？

19．一次函数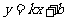的图象过点(，5)，并且与y轴相交于点P，直线

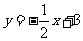
与y轴相交于点Q，点Q与点P关于x轴对称，求这个一次函数的解析式．

18．已知，函数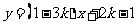，试回答：

(1)k为何值时，图象交x轴于点(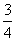，0)？

(2)k为何值时，y随x增大而增大？

(3)k为何值时，图象过点(，)．

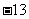17．已知，直线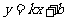经过点A(3，8)和B(，)．求：

(1)k和b的值；

(2)当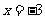时，y的值．

www.1230.org 初中数学资源网