
3.可用平稳时的频率估计这一事件在每次抛掷时发生的可能性,即机会。
2.发现只要保持实验条件不变,那么随机事件发生的频率也会表现出规律:即在相同条件下随着实验次数的增加,事件出现的频率逐渐趋于稳定,稳定到某一个数值。
2.准备30张小卡片,上面分别写好数1到30,然后将卡片放在袋子里搅匀。每次从袋中取出一张卡片,记录结果,然后放回搅匀再抽。
(1)将实验结果填人下表。
|
实验次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
出现3的倍数的频数 |
|
|
|
|
|
|
|
|
|
|
|
出现3的倍数的频率 |
|
|
|
|
|
|
|
|
|
|
(2)根据上表中的数据绘制折线图。 (3)在实验数据中发现了什么规律? (4)频率稳定于什么值? (5)知道从一个袋中取出一张卡片是3的倍数的机会是多少?
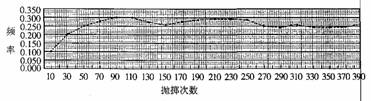
1.以下是某位同学在做400次抛掷两枚硬币的实验时,根据“出现两个正面”的成功率,画出的折线图。(横坐标表示实验总次数,纵坐标表示实验成功率。)
(1)我们可以看到,随着实验的次数的增加,成功率是这样变化的:_______
(2)因为成功率有趋于稳定的特点,所以我们以后就用平稳时的成功率表示某一事件发生的_____,即_____。
(3)可以看到当实验进行到260次后,所得频率值就在____上下浮动,所以我们可以得到“机会大约是______”的粗略估计。
2.判断。
(1)某彩票的中奖机会是1/22,那么某人买22张彩票,肯定有一张中奖。 ( )
(2)抛掷一枚质量分布均匀的硬币,出现"iE面”和“反面”的机会均等。因此,抛1 000次的话,一定会有500次“正”,500次“反”。 ( )七、拓展延伸、开放性练习。
1.填空。
(1)观察大量的反复实验后获得的频率的折线统计图,发现只要保持实验条件不变,那么,随机事件发生的频率也会表现出规律:即随着相同条件下实验次数的增加,其值逐渐稳定到_____。我们可以用平稳时的频率估计这一事件发生的可能性,即_______。
(2)抛掷一枚硬币的实验中,出现正面的机会是_____。
(3)抛掷两枚硬币的实验中,随着实验次数的增加出现两个正面的频率将逐渐稳定在_____左右。出现-正一反的频率将逐渐稳定在______左右。
4.不能用图钉代替,因为用图钉代替改变了实验的条件。
3.实验2中,出现两个正面的频率约是25%,出现一正一反的频率约是 50%。比较稳定。
2.频数具体是多少不确定。但是在实验中,抛掷400次时频数约是200次,频率约是50%。
抛掷800次时频数约是400次,频率约是50%。
随着相同条件下实验次数的增加,其值逐渐趋于稳定,稳定到50%左右。
1.具有不确定性,因为抛掷硬币是随机事件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com