4．下列计算正确的是(　 )

　　 A．(8a³b⁸)÷(4ab⁴)=2a²b²　　　 B．(8a³b⁸)÷(4ab⁴)=2a³b⁴

　　 C．(-2x²y⁴)÷(-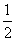xy²)=xy²　　 D．(-a⁴b⁵c)÷(a²b³)=-a²b²c

3．(05年江苏省海安市中考)计算(-3a³)²÷a²的结果为(　 )

　　 A．9a⁴　　　 B．-9a⁴　　 C．6a⁴　　 D．9a³

2．x²y³÷(xy)²的结果是(　 )

　　 A．xy　　　 B．x　　　 C．y　　 D．xy²

1．计算(14a³b²-21ab²)÷7ab²等于(　 )

　　 A．2a²-3　　 B．2a-3　　 C．2a²-3b　　 D．2a²b-3

2．预习“多项式与单项式的除法．”

　 《三级训练》

1．课本习题15．4─2、4、5题．

2．应用单项式除法法则应注意：

　　 ①系数先相除，把所得的结果作为商的系数，运算过程中注意单项式的系数饱含它前面的符号；

　　 ②把同底数幂相除，所得结果作为商的因式，由于目前只研究整除的情况，所以被除式中某一字母的指数不小于除式中同一字母的指数；

　　 ③被除式单独有的字母及其指数，作为商的一个因式，不要遗漏；

　　 ④要注意运算顺序，有乘方要先做乘方，有括号先算括号里的，同级运算从左到右的顺序进行．

　　 Ⅴ．课后作业

1．单项式的除法法则是_________________．

1．例：计算

　　 (1)28x⁴y²÷7x³y

　　 (2)-5a⁵b³c÷15a⁴b

　　 (3)(2x²y)³·(-7xy²)÷14x⁴y³

　　 (4)5(2a+b)⁴÷(2a+b)²

　　 分析：(1)、(2)直接运用单项式除法的运算法则；(3)要注意运算顺序：先乘方，再乘除，再加减；(4)鼓励学生悟出：将(2a+b)视为一个整体来进行单项式除以单项式的运算．

　　 解：(1)28x⁴y²÷7x³y

　　 =(28÷7)·x^4-3·y^2-1

　　 =4xy．

　　 (2)-5a⁵b³c÷15a⁴b

　　 =(-5÷15)a^5-4b^3-1c

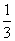　　 =-ab²c．

　　 (3)(2x²y)³·(-7xy²)÷14x⁴y³

　　 =8x⁶y³·(-7xy²)÷14x⁴y³

　　 =[8×(-7)]·x⁶⁺¹y³⁺²÷14x⁴y³

　　 =(-56÷14)·x^7-4·y^5-3

　　 =-4x³y²．

　　 (4)5(2a+b)⁴÷(2a+b)²

　　 =(5÷1)(2a+b)^4-2

　　 =5(2a+b)²

　　 =5(4a²+4ab+b²)

　　 =20a²+20ab+5b²

　　 Ⅲ．随堂练习

　　 a．课本P189练习1、2．

　Ⅳ．课时小结

2．还可以从除法的意义去考虑．

　　 (1)(1.90×10²⁴)÷(5.98×10²¹)=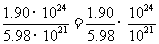=0．318×10³．

　　 (2)8a³÷2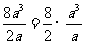a==4a．

　　　　 6x³y÷3xy=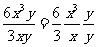=2x²．

　　　　 12a³b²x³÷3ab²=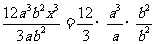·x³=4a²x³．

　　 上述两种算法有理有据，所以结果正确．

　　 [师]请大家考虑运算结果与原式的联系．

　　 [生甲]观察上述几个式子的运算，它们有下列共同特征：

　　 (1)都是单项式除以单项式．

　　 (2)运算结果都是把系数、同底数幂分别相除后作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式．

　　 (3)单项式相除是在同底数幂的除法基础上进行的．

　　 [生乙]其实单项式除以单项式可以分为系数相除；同底数幂相除，只在被除式里含有的字母三部分运算．

　　 [师]同学们总结得很好．能用很条理的语言描述单项式与单项式相除的运算法则，而且能抓住法则的实质所在，这是数学能力的提高与体现，老师为你们骄傲．下面我们应用单项式与单项式相除的运算法则解决一些计算问题，进一步体会运算法则的实质所在．