1．师生共同研究教科书第174页的问题，对单项式与多项式相乘的方法能有感性认识．

***这个实际问题来源于学生的生活实际，所以在教学中通过师生共同探讨，再结合分配律学生不难得到结论．

4．辩一辩教科书第174页练习2

***辩一辩的目的是让学生通过对这些判断题的讨论甚至争论，加强对运算法则的掌握，同时也培养学生一定的批判性思维能力．

深入探究

3．算一算例1教科书第173页例4

在例题教学中应该先让学生观察有哪些运算，如何利用运算性质和法则。分析后再动手做，同时让学生说一说每一步的依据．提醒学生在单项式的运算中应该先确定符号．

例2 小民的步长为a米，他量得家里的卧室长15步，宽14步，这间卧室的面积有多少平方米?

***将运算法则应用在实际问题中，提高学生解决实际问题的能力．

2．试一试：

类似地，请你试着计算：(1)2c⁵·5c²；(2)(-5a²b³)·(-4b²c)

ac⁵和bc²，2c⁵和5c²，(-5a²b³)和(-4b²c)都是单项式，通过刚才的尝试，谁能告诉大家怎样进行单项式乘法?

***先不给出单项式与单项式相乘的运算法则，而是让学生类比，自己动手试一试，再相互交流，自己小结出如何进行单项式的乘法．要求学生用语言叙述这个性质，这对于学生提高数学语言的表述能力是有益的．

学生小结：单项式与单项式相乘，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．

1．问题：如果将上式中的数字改为字母，即ac⁵·bc²，你会算吗?

学生独立思考，小组交流．

***从特殊到一般，从具体到抽象，在这一过程中，要注意留给学生探索与交流的空间，让学生在自己的实践中获得单项式与单项式相乘的运算法则．

学生分析：跟刚才的解决过程类似，可以将ac⁵和bc²分别看成a·c⁵和b·c²，再利用乘法交换律和结合律．

ac⁵·bc²

=(a·c⁵)·(b·c²)

=(a·b)·(c⁵·c²)

=abc⁵⁺²

=abc⁷

***在教学过程中注意运用类比的方法来解决实际问题．

2．练一练

口答：

幂的三个运算性质是学习单项式与单项式、单项式与多项式乘法的基础，所以先组织学生对上述内容做复习．

创设情境引入新课

问题光的速度约为3×10⁵千米/秒，太阳光照射到地球上需要的时间大约是5×10²秒，你知道地球与太阳的距离约是多少千米吗?

***从实际的问题导入，让学生自己动手试一试，主动探索，在自己的实践中获得知识，从而构建新的知识体系．

地球与太阳的距离约为(3×10⁵)×(5×10²)千米．问题是(3×10⁵)×(5×10²)等于多少呢?学生提出运用乘法交换律和结合律可以解决：

(3×10⁵)×(5×10²)=(3×5)×(10⁵×10²)=15×10⁷(为什么?)

在此处再问学生更加规范的书写是什么?应该是地球与太阳的距离约为1.5×lO8千米．

请学生回顾，我们是如何解决问题的．

探究新知

1．知识回顾：

回忆幂的运算性质：

a^m·aⁿ=a^m+n(m，n都是正整数)

即同底数幂相乘，底数不变，指数相加．

(a^m)ⁿ=a^mn(m，n都是正整数)

即幂的乘方，底数不变，指数相乘．

(ab)ⁿ=aⁿbⁿ(n为正整数)

即积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘．

15.2整式的乘法(2)

教学目标:

①探索并了解单项式与单项式、单项式与多项式相乘的法则，并运用它们进行运算．

②让学生主动参与到探索过程中去，逐步形成独立思考、主动探索的习惯，培养思维的批判性、严密性和初步解决问题的愿望与能力．

教学重点与难点

重点：单项式与单项式、单项式与多项式相乘的法则．

难点：单项式与多项式相乘去括号法则的应用．

教学设计

复习引新

1．必做题：教科书第177页习题15.2第1、2题．2．备选题：

(1)计算：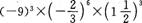

(2)计算：a^m-1·aⁿ⁺²+a^m+2·a^n-1+a^m·aⁿ⁺¹

(3)已知：a^m=7，b^m=4，则(ab)^2m=______

(4)已知：3^x+2^y-3=0，则27^x·9^y=___________

设计思想

本节课需要掌握三个运算性质：“同底数幂的乘法”、“幂的乘方”和“积的乘方”，这三个运算性质是整式乘法运算的基石，又是在幂的意义的基础上发展的．教师以“计算与问题-观察与猜想-归纳与概括”为教学主线引导学生探索运算性质，淡化推理论证，强调留给学生探索与交流的空间，重视性质的探索过程和数学感受．通过设置问题情境和操作情境，运用乘方的意义进行有理数的幂的乘法，让学生在主动的探索中获得同底数幂的乘法运算性质，再通过学生的动手实践，运用乘方的意义、同底数幂的乘法运算性质和乘法运算律自主获得幂的乘方、积的乘方运算性质，突破难点，从而构建新的知识体系．

对于容易混淆的概念，诸如“a³+a³与a³·a³，a²·a³与(a²)³”之类的问题，通过组织学生讨论和辨析，加强对幂的运算的掌握，同时也培养了一定的思维批判性．

在课堂教学中，通过口答、动手做一做等，组织学生进行比赛，培养学生一定的计算能力．在具体实施中，采用小组学习的方式，培养学生的合作意识；引导全班同学一起探索、交流与讨论，在激发了学生的学习热情的同时，获得知识的提升．

9．做一做

例3教科书第172页的例3(1)-(4);补充：(5) [-3(x+y)²]³

例4　 计算：x·(x²)³-2x⁴·x²

比一比

这节课我们学习了三个运算性质：“同底数幂的乘法”、“幂的乘方”和“积的乘方”．组织学生进行计时比赛，在规定时间内完成教科书第170页、17l页、172页的练习．

深入探究例5计算：(1)(-8)²⁰⁰⁴·(-0.125)²⁰⁰⁵(2)(-2)²ⁿ⁺¹+2·(-2)²ⁿ(n为正整数)．

在这三个性质中的底数、指数中，指数注明为正整数，而底数可以是数、字母或式．把底数进一步扩充到式的范围．

议一议

下面的计算对不对?如果不对，应当怎样改正．

(1)a³·a³=a⁶；

(2)b⁴·b⁴=2b⁴；

(3)x⁵+x⁵=x¹⁰;

(4)y⁷·y=y⁸；

(5)(a³)⁵=a⁸；

(6)a³·a⁵=a¹⁵;

(7)(a²)³·a⁴=a⁹；

(8)(xy³)²=xy⁶；

(9)(-2x)³=-2x³

***补充议一议与辨析题的目的是让学生通过对这些判断题的讨论甚至争论，加强对运算性质的掌握，同时也培养学生一定的批判性思维能力．

小结

组织学生讨论和辨析三个运算性质．

课外巩固