1． P31思考提出问题，引发学生的思考，从而引出解分式方程的解法以及产生增根的原因.

3．认知难点与突破方法

　 解可化为一元一次方程的分式方程，也是以一元一次方程的解法为基础，只是需把分式方程化成整式方程，所以教学时应注意重新旧知识的联系与区别，注重渗透转化的思想，同时要适当复习一元一次方程的解法。至于解分式方程时产生增根的原因只让学生了解就可以了，重要的是应让学生掌握验根的方法.

要使学生掌握解分式方程的基本思路是将分式方程转化整式方程，具体的方法是“去分母”，即方程两边统称最简公分母.

要让学生掌握解分式方程的一般步骤：

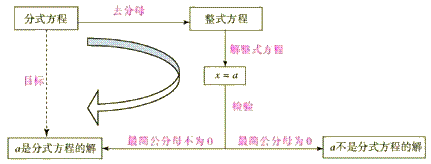
2．难点：会解可化为一元一次方程的分式方程，会检验一个数是不是

原方程的增根.

1．重点：会解可化为一元一次方程的分式方程，会检验一个数是不是

原方程的增根.

2．掌握分式方程的解法，会解可化为一元一次方程的分式方程，会检

验一个数是不是原方程的增根.

1．了解分式方程的概念, 和产生增根的原因.

16．3分式方程(一)

2.(1) 1.2×10^-5 　(2)4×10³　

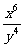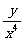2.(1)　 (2)　 (3)　

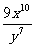
2.计算

(1) (3×10^-8)×(4×10³)　　　　 (2) (2×10^-3)²÷(10^-3)³