6.如图2，梯形的上底AD=3 cm，下底BC=6 cm，对角线AC=9 cm，设OA=x，则x=_________ cm.

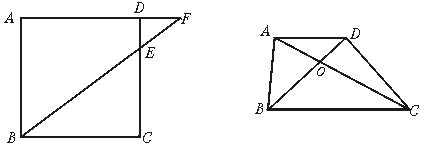
图1 　　　　　　　　　　　　　　　　 　图2

5.如图1，在正方形ABCD中，AB是4 cm，△BCE的面积是△DEF面积的4倍，则DE的长为_________.

4.将长为5，宽为4的矩形，沿四个边剪去宽为x的4个小矩形，剩余部分的面积为12，则剪去小矩形的宽x为_________.

3.为了利用配方法解方程x²－6x－6=0，我们可移项得___________，方程两边都加上_________，得_____________，化为___________.解此方程得x₁=_________，x₂=_________.

2.求下列方程的解

①x²+4x+3=0___________

②x²+6x+5=0___________

③x²－2x－3=0___________

1.填写适当的数使下式成立.

①x²+6x+______=(x+3)²

②x²－______x+1=(x－1)²

③x²+4x+______=(x+______)²

2.会设计与一元二次方程有关的实际问题

班级：___________________________姓名：___________________________

作业导航

1.会用配方法解一元二次方程

2.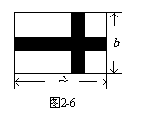如图2-6，某中学有一块长a米，宽b米的矩形场地，计划在该场地上修筑宽都为2米的两条互相垂直的道路，余下的四块矩形小场地建成草坪. 已知，a︰b = 2︰1, 且四块草坪的面积之和为312米²，求原矩形场地的长与宽各为多少米.

[综合练习]

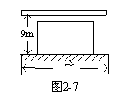建一个面积为150米²的长方形养鸡场，为节省材料，鸡场的一边靠着原有的一面墙(如图2-7)，墙长为a米，另三边用篱笆围成，已知篱笆总长为35米，

(1)求鸡场的长与宽各多少米；

(2)题中墙的长度a对问题的解起着怎样的作用？

若离墙9米开外准备修路，那么a的长度至少

要有多少米？

练习三

[基础练习]一、1. (x -5)² = 36； 2. 26，27； 3. 12,15.　 二、1. C； 2. D. 三、1.5米. 2. a = 28米, b = 14米.

[综合练习](1)当a<15时，问题无解；当15≤a<20时，长为15米，宽为10米；当a≥20时，长为15米，宽为10米或长为20米，宽为7.5米；(2)a对问题的解起着限制作用；a的长度至少要有20米.

1.某大学为改善校园环境，计划在一块长80米，宽60米的矩形场地中央建一个矩形网球场，网球场占地面积为3500平方米，四周为宽度相等的人行步道. 求人行步道的宽度.