
x2+5x+2=0.
解:把常数项移到方程的右边,得
x2+5x=-2.
两边都加上(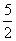 )2,得
)2,得
x2+5x+(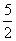 )2=-2+(
)2=-2+(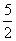 )2,
)2,
即(x+ 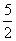 )2=
)2=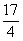 .
.
两边同时开平方,得
x+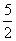 =±
=±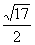 ,
,
即x+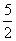 =
=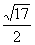 或x+
或x+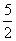 =-
=-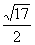 .
.
所以x1=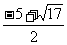 ,x2=
,x2=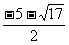 .
.
x2+12x=15,
x2+12x+62=15+62,
即(x+6)2=51,
x+6=±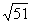 ,
,
即x+6=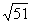 或x+6=-
或x+6=-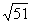 ,
,
x1=-6+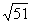 ,x2=-6-
,x2=-6-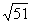 (舍).
(舍).
梯子底端滑动的距离是(-6+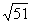 )米.这种解一元二次方程的方法称为配方法.
)米.这种解一元二次方程的方法称为配方法.
例1:解方程x2+8x-9=0
x=±2.
(2)(x+3)2=9,
x+3=±3,
x+3=3或x+3=-3,
x1=0,x2=-6.
这种方法叫直接开平方法.
(x+m)2=n(n≥0).
2.难点:配方过程中,解一元二次方程的要点的理解。
1.重点:运用配方法解简单的数字系数的一元二次方程。
3.能说出用配方法解一元二次方程的基本步骤.
情感态度与价值观目标:
通过用配方法将一元二次方程变形的过程,让学生进一步体会转化的思想方法,并增强他们的数学应用意识和能力.
重点、难点、关键:
2.会用配方法解简单的数字系数的一元二次方程.
1.理解配方法;知道“配方”是一种常用的数学方法.
2.了解用配方法解一元二次方程的基本步骤.
过程与方法目标:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com