
2.下列方程属于一元二次方程的是( )
(A)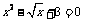 (B)
(B)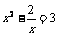 (C)
(C)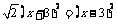 (D)
(D)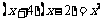
 3 下列图案中,不是中心对称图形的是 ( )
3 下列图案中,不是中心对称图形的是 ( )
1.下列各式中属于最简二次根式的是 ( )
(A)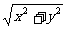 (B)
(B)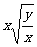 (C)
(C)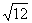 (D)
(D)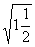
27、(本题满分12分):
 (1)、当∠POA=90°时,点P运动的路程为
(1)、当∠POA=90°时,点P运动的路程为
⊙O周长的 或
或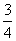 。
。
设点P运动的时间为ts
当点P运动的路程为⊙O周长的 时,
时,
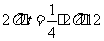 解得 t=3;………(2分)
解得 t=3;………(2分)
当点P运动的路程为⊙O周长的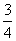 时,
时,
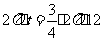 解得 t=9
解得 t=9
∴ 当∠POA=90°时,点P运动的时间为3s或9s。……………(4分)
(2)、如图,当点P运动的时间为2s时,直线BP与⊙O相切。……(5分)
理由如下:
当点P运动的时间为2s时,点P运动的路程为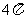 cm。
cm。
连接OP、PA
∵ ⊙O的周长为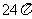 cm ∴
cm ∴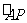 的长为⊙O周长的
的长为⊙O周长的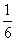 。
。
∴ ∠POA=60°…………………………………(7分)
∵ OP=OA , ∴△OAP是等边三角形
∴ OP=OA=AP, ∠OAP=60° ………………………(8分)
∵ AB=OA,∴ AP=AB
∵ ∠OAP= ∠APB+∠B。 ∴ ∠APB=∠B=30°
∴ ∠OPB=∠OPA+∠APB=90°……………………(10分)
∴ OP⊥BP。
∴ 直线BP与⊙O相切。……………………………(12分)
26、(本题满分10分):
(1)、描点及所画⊙P如图所示 ……………………(3分)
由图可知:在Rt△ABC中,AB=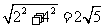 ……………(4分)
……………(4分)
∴ ⊙P的半径为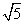 ,又 PD=
,又 PD=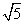
∴ 点D在⊙P上。 ………………………………(5分)
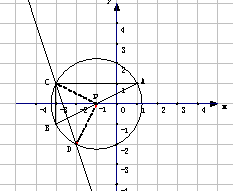 (2)、连接PC、PD
(2)、连接PC、PD
∵ PC=PD=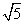 ,CD=
,CD=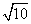
∴ 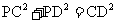
∴ ∠CPD=90°………………(7分)
∴ s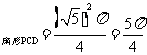 ,
,
s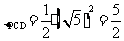 …………(9分)
…………(9分)
∴ 直线CD与⊙P的劣弧CD围成的图形的面积为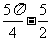 ……… (10分)
……… (10分)
25、(本题满分10分):
(1)、证明:连接OC…………………………………(1分)
∵ OA=OB AC=BC
∴ △OAB是等腰三角形,OC是底边AB上的中线……(2分)
∴ OC⊥AB………………………………(3分)
∴ AB是⊙O的切线 …………………(4分)
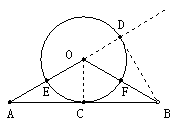 (2)、作BD⊥AD,交AO的延长线于D
(2)、作BD⊥AD,交AO的延长线于D
∵ BD=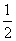 AB ∴ ∠OAB=30° …………(5分)
AB ∴ ∠OAB=30° …………(5分)
∵ OA=OB ∴ ∠OAB=∠OBA
∴ ∠AOB=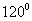
∵ AB= ∴ BD=AC=BC=
∴ BD=AC=BC=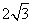 ………(6分)
………(6分)
设⊙O的半径OC=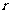 ,则OA=
,则OA=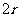
由勾股定理,得  +
+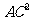 =
=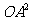 即
即 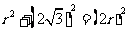
解得, r=2 ………………(8分)
∴ 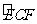 的弧长为
的弧长为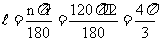 ………(10分)
………(10分)
24、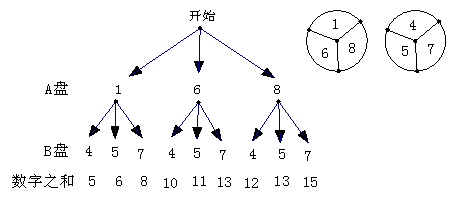 (本题满分8分):
(本题满分8分):
补全树形图(4分),
游戏中共有9种可能出现的结果,且这些结果出现的可能性相等,其中数字相加为偶数的,即小明获胜有4种结果,即6、8、10、12,………………………(6分)
所以 P(小明获胜)= ……… ……… (8分)
……… ……… (8分)
23、(本题满分8分):
解:设每件童装应降价X元,则平均每天多售出2X件(1分
(20+2X)(40-X)=1200 …………………………(4分)
整理,得 X2-30X+200=0……………………………(5分)
解方程,得 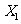 =10 ,
=10 ,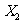 =20………………………(7分)
=20………………………(7分)
答:每件童装应降价10元或20元。……………………(8分)
22、(本题满分10分):
(1)、作出△ ,如图所示:……(4分)
,如图所示:……(4分)
 (2)、由已知条件,得
(2)、由已知条件,得
 =
=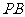 ,∠
,∠ =90°……(6分)
=90°……(6分)
∴ △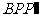 是等腰直角三角形。
是等腰直角三角形。
作PE⊥BC于E,则BE=3,PE=4
∴ PB=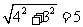 ……………………(7分)
……………………(7分)
在Rt△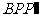 中,
中, =
=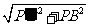 =
=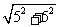 =5
=5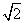 …………(8分)
…………(8分)
∴ △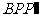 的周长是
的周长是 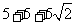 =
= ,…………………(9分)
,…………………(9分)
S△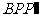 =
=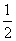 ×
×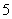 ×
×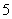 =
=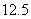 ……………………………………(10分)
……………………………………(10分)
21、计算:(每小题7分,满分14分)
(1)、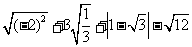
解:原式=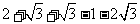 ………………………(4分)
………………………(4分)
= 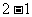 …………………………………………(6分)
…………………………………………(6分)
= 1 …………………………………………(7分)
(2)、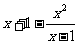
 =
=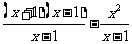 …………(2分)
…………(2分)
=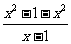 ……………………(4分)
……………………(4分)
=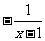 …………………………(5分)
…………………………(5分)
当 =
=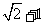 时, 原式=
时, 原式=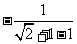 =
=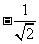 =
=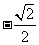 ………………………(7分)。
………………………(7分)。
20、(1)、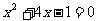 (此题有多种解法)
(此题有多种解法)
解:移项,得: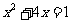 ………………………(1分)
………………………(1分)
配方, 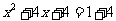 ……………………(3分)
……………………(3分)
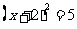 ……………………………(4分)
……………………………(4分)
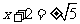 ……………………………(5分)
……………………………(5分)
∴  ,
,  ………………(7分)
………………(7分)
(2)、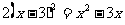
解:移项,得 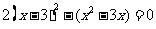 ……(2分)
……(2分)
因式分解,得
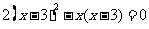 ……(3分)
……(3分)
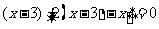 …………………(4分)
…………………(4分)
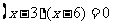 ………………………(5分)
………………………(5分)
于是得 x-3=0或x-6=0 ………………………(6分)
∴ x1=3, x2=6 ……………………………(7分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com