
4、 下列图案中,不是中心对称图形的是
下列图案中,不是中心对称图形的是
3. 下列方程属于一元二次方程的是
(A)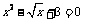 (B)
(B)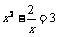 (C)
(C)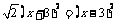 (D)
(D)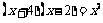
2.下列各式中属于最简二次根式的是
(A)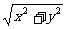 (B)
(B)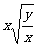 (C)
(C)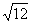 (D)
(D)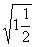
1.如果a为任意实数,下列根式一定有意义的是:
(A)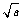 (B)
(B)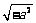 (C)
(C)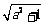 (D)
(D)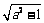
23、 (15分)已知,如图:在平面直角坐标系中,点D是直线y=-x上一点,过O、D两点
 的圆⊙O1分别交X轴、Y轴于点A和B,
的圆⊙O1分别交X轴、Y轴于点A和B,
(1)、当A(-12,0),B(0,-5)时,求O1的坐标;
(2)、在(1)的的条件下,过点A作⊙O1的切线与BD的延长线相交于点C,
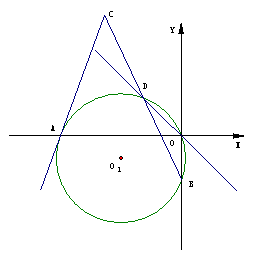 求点C的坐标;
求点C的坐标;
(3)、若点D的横坐标为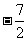 ,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O1的大小发生变化时,其结论:AE-BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围。
,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O1的大小发生变化时,其结论:AE-BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围。
2008~2009学年度第一学期期中考试
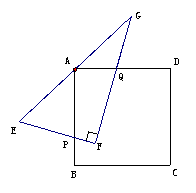
24、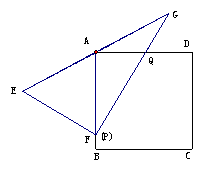 (15分)已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:
(15分)已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:
(1),求证:EP2+GQ2=PQ2
 (2)、若将Rt△EFG绕着点A逆时针旋转
(2)、若将Rt△EFG绕着点A逆时针旋转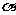 (0°<
(0°<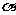 ≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论。若不存在,请说明理由。
≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论。若不存在,请说明理由。
 (3)、若将Rt△EFG绕着点A逆时针旋转
(3)、若将Rt△EFG绕着点A逆时针旋转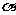 (90°<
(90°<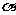 <180°),两直角边分别交AB、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明)。
<180°),两直角边分别交AB、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明)。
23.(本题10分)已知:如图,Rt△ABC,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D
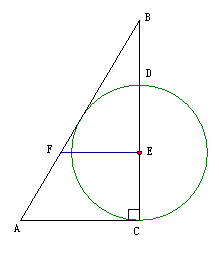 (1)、求证:斜边AB是⊙E的切线;
(1)、求证:斜边AB是⊙E的切线;
(2)、设若AB与⊙E相切的切点为G, AC=8,EF=5,连DA、DG,求S△ADG;
22.(10分)某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积
(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个
村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为60000元.
(1).一年中这个村修建了多少公顷蔬菜大棚?
(2).若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.
21、(10分)如图,已知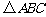 的顶点
的顶点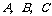 的坐标分别是A(-1,-1)
的坐标分别是A(-1,-1)
B(-5,-4)C(-5,-1).
(1)、作出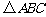 关于点P(0,-2)中心对称的图形
关于点P(0,-2)中心对称的图形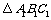 ,
,
并直接写出顶点A1、B1、C1的坐标.
(2)、将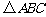 绕原点O按顺时针方向旋转90°后得到△A2B2C2,
绕原点O按顺时针方向旋转90°后得到△A2B2C2,
画出△A2B2C2,并直接写出顶点A2、B2、C2的坐标.
(3)、将 沿着射线BA的方向平移10个单位,后得到△A3B333
沿着射线BA的方向平移10个单位,后得到△A3B333
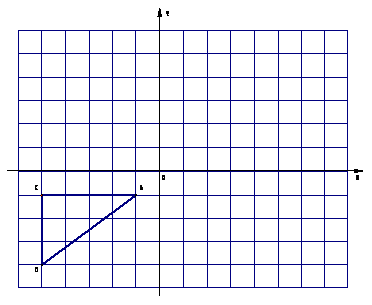 画出△A3B3C3,并直接写出顶点A3、B3、C3的坐标.
画出△A3B3C3,并直接写出顶点A3、B3、C3的坐标.
20.(本题10分)水厂为了了解绿园小区居民的用水情况,随机抽查了该小区10户家庭八月份的用水量,结果如下:
|
月用水量(吨) |
10 |
13 |
15 |
17 |
19 |
|
户数 |
2 |
2 |
3 |
2 |
1 |
(1)计算这10户家庭八月份的平均用水量;
(2)由于小区居民增强了环保节水意识,九月和十月的用水量逐月下降.到十月份这10户家庭的用水量为100m3,求这两个月用水量的平均下降率.(精确地千分位)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com