(三)圆和圆的位置关系

　　 1.记住5种位置关系的圆心距d与两圆半径之间的相等或不等关系.会利用d与R,r之间的关系确定两圆的位置关系,会利用d,R,r之间的关系确定两圆的位置关系.

2.相交两圆,添加公共弦,通过公式弦将两圆连结起来.

　 相切两圆,添加公切线,利用两圆的公切线将两圆连结起来.

3.公切线的长的计算

　　　　　　　　　　　　 A　　　　 B

　　　　　　　　　　　　　　　　　　　　　　　　 L

　　　　　　　　　　 O₁　　　　　　 O₂ R-r

　　　 　　　　　　　　　　　　　　　　　　　　　d

外公切线：

两圆半径差R-r,公切线的长L分别是Rt△的两直角边，圆心距d是斜边.

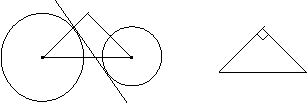内公切线：　　　　　　

　　　　　　　　　　　　　　　　　　　　 R+r　　　 l

　　　　　　　　　　　　　　　　　　　　　　　 d

两圆半径和R+r,内公切线L和圆心距d构成直角三角形.

可围绕这个三角形的三边进行计算.

(二)直线和圆的位置关系

　　 1.性质:圆的切线垂直于经过切点的半径.(有了切线,将切点与圆心连结,则半径与切线垂直,所以连结圆心和切点,这条辅助线是常用的.)

2.切线的判定有两种方法.

①若直线与圆有公共点,连圆心和公共点成半径,证明半径与直线垂直即可.

②若直线和圆公共点不确定,过圆心做直线的垂线,证明它是半径(利用定义证)。根据不同的条件,选择不同的添加辅助线的方法是极重要的.

3.三角形的内切圆:内心是内切圆圆心,具有的性质是:到三角形的三边距离相等,还要注意说某点是三角形的内心.

连结三角形的顶点和内心,即是角平分线.

4.切线长定理:自圆外一点引圆的切线，则切线和半径、圆心到该点的连线组成直角三角形,还要注意,　　　　　　　　　　 A

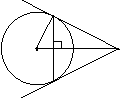图形中有射影定理的基本图形.

　　　　　　　　　　　　　　　　　 O　 D　　　 P

　　　　　　　　　　　　　　　　　　 B

5.弦切角是与圆有关的第三种角,当条件是切线时,往往找弦切角,看弦切角所对的弧,再找弧所对的圆周角得两角相等.

6.和圆有关的比例线段：理解定理,会用.

(一)圆的有关性质,本节中最重要的定理有4个.

　　 1.垂径定理:本定理和它的三个推论说明: 在(1)垂直于弦(不是直径的弦);(2)平分弦;(3)平分弦所对的弧;(4)过圆心(是半径或是直径)这四个语句中,满足两个就可得到其它两个的结论.如垂直于弦(不是直径的弦)的直径,平分弦且平分弦所对的两条弧。条件是垂直于弦(不是直径的弦)的直径，结论是平分弦、平分弧。再如弦的垂直平分线,经过圆心且平分弦所对的弧。条件是垂直弦,、分弦,结论是过圆心、平分弦.

应用:在圆中,弦的一半、半径、弦心距组成一个直角三角形,利用勾股定理解直角三角形的知识,可计算弦长、半径、弦心距和弓形的高.

2.圆心角、弧、弦、弦心距四者之间的关系定理：在同圆和等圆中, 圆心角、弧、弦、弦心距这四组量中有一组量相等,则其它各组量均相等.这个定理证弧相等、弦相等、圆心角相等、弦心距相等是经常用的.

3.圆周角定理：此定理在证题中不大用,但它的推论,即弧相等所对的圆周角相等；在同圆或等圆中,圆周角相等,弧相等.直径所对的圆周角是直角,90°的圆周角所对的弦是直径,都是很重要的.条件中若有直径,通常添加辅助线形成直角.

4.圆内接四边形的性质:略.

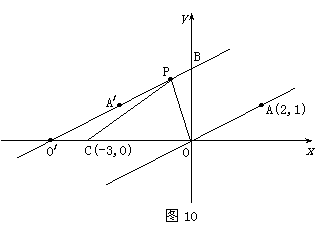
24．(12分)已知正比例函数y=kx经过点A(2,1)，如图10所示．

(1)求这个正比例函数的关系式.

(2)将这个正比例函数的图像向左平移4个单位，写出在这个平移下，点A、原点O的对应点A^/、O^/的坐标，求出平移后的直线O^/A^/所对应的函数关系式.

　(3)已知点C的坐标为(-3,0)，点P(x,y)为线段O^/B上一动点(P与O^/、B不重合)，设△PCO的面积为S.

　　　　 ① 求S与x之间的函数关系式及x的取值范围；

　　　　 ② 求当S=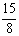时，点P的坐标.

2007-2008学年度第二学期

23.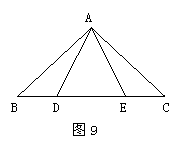 (10分)如图9，E、D是△ABC中BC边上的两点，AD=AE，请添加一个条件，使图中存在全等三角形并给予证明．

你所添加的条件为：　　　　　　　　　　　 ；

得到的一对全等三角形是△______≌△______．

证明：

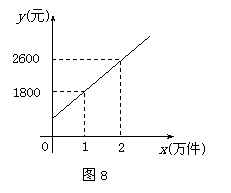
22．(10分)某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系，其图象如图8所示. 根据图象提供的信息，解答下列问题：

(1)求出营销人员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式；

(2)该公司营销人员的底薪是(没有销售量时的收入)多少元？

(3)已知该公司营销员李明5月份的销售量为1.2万件，求李明5月份的收入.

21．(8分)现要装配30台机器，在装配好6台后，采用了新的技术，每天的工作效率提高了一倍，结果共用了3天完成了任务. 求采用新的技术后每天能装多少台机器.

20．(6分) 解方程：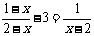

19．(第(1)小题4分，第(2)小题6分，共10分)

(1)请从下列三个代数式中任选两个构造一个分式，并化简该分式．

, , ．

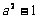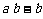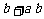(2)先化简，再求值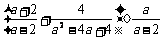：，其中.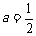

18． 如图7，在△ABD和△ACE中，有下列四个论断：①AB=AC；②AD=AE；③∠B=∠C；④BD=CE.

　 　请以其中三个论断作为条件，余下一个论断作为结论，写出一个真命题是　　 　　　.