
(二)填空题:
1.若圆的半径是2cm,一条弦长是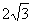 ,则圆心到该弦的距离是______.
,则圆心到该弦的距离是______.
2.在⊙O中,弦AB为24,圆心到弦的距离为5,则⊙O的半径是______cm.
3.若AB是⊙O的直径,弦CD⊥AB于E,AE=9cm,BE=16cm,则CD=______cm.
4. 若⊙O的半径是13cm,弦AB=24cm,弦CD=10cm,AB∥CD,则弦AB与CD之间的距离是______cm.
5. ⊙O的半径是6,弦AB的长是6,则弧AB的中点到AB的中点的距离是______.
6.
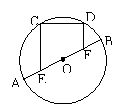
 如图:⊙O的直径AB⊥CD于P,
如图:⊙O的直径AB⊥CD于P,
AP=CD=4cm,则OP=______cm.
7. 已知⊙O中,AB是弦,CD是直径,且CD⊥AB于M.⊙O的半径是15cm,OM:OC=3:5,则AB=______.
8.
已知O到直线l的距离OD是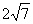 cm,l上一点P,PD=
cm,l上一点P,PD=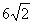 cm.⊙O的直径是20,则P在⊙O______.
cm.⊙O的直径是20,则P在⊙O______.
 (三)证明题:
(三)证明题:
1.如图:AB是⊙O的直径,CD是弦
CE⊥CD于C,DF⊥CD于D
求证:AE=BF
2.⊙O和⊙O1相交于A,B.过A做CAD∥OO1
 求证:CD=2OO1
求证:CD=2OO1
(一)判断题
1.直径是弦.( )
2.半圆是弧,但弧不一定是半圆. ( )
3.到点O的距离等于2cm的点的集合是以O为圆心,2cm为半径的圆. ( )
4.过三点可以做且只可以做一个圆. ( )
5.三角形的外心到三角形三边的距离相等. ( )
6.经过弦的中点的直径垂直于弦,且平分弦所对的两条弧. ( )
7.经过圆O内一点的所有弦中,以与OP垂直的弦最短. ( )
8.弦的垂直平分线经过圆心. ( )
9.⊙O的半径是5,弦AB∥CD,AB=6,CD=8,则两弦间的距离是1. ( )
10.在半径是4的圆中,垂直平分半径的弦长是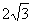 .( )
.( )
11.任意一个三角形一定有一个外接圆且只有一个外接圆. ( )
3.垂径定理:是圆中一个极重要的定理.
垂径定理:垂直于弦的直径平分弦且平分弦所对的两条弦.
推论(1):平分弦(不是直径)的直径垂直于弦,且平分弦所对的两条弦(注意括号内的条件)
(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
(3):平分弦所对的一条弧的直径,垂直平分弦且平分弦所对的另一条弧.
 此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2)
此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2)
注意:题设是两条,如
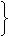 ∵AB是直径
∵AB是直径
AB⊥CD于E
∴CE=DE
弧AC=弧DA 弧BC=弧DB
具体做题时,辅助线往往过圆心做弦的垂线段.连结圆心,则半径,弦的一半,圆心到弦的距离形成一个RtΔ,则可用勾股定理,锐角三角函数进行计算或证明.
2.过一点的圆有无数个,它的圆心是平面上除A外所有点.过两点的圆有无数个,它们的圆心在AB的垂直平分线上.过三点呢?若这三点不在同一直线上,过三点可以做且只可以做一个圆.(但这三点在同一直线上,则不能过三点作圆).
若把三点连结起来,构成三角形,则经过三角形各顶点的圆叫三角形的外接圆.
外接圆的圆心叫三角形外心.外心的性质是到三角形各顶点的距离相等.
三角形的外接圆的做法:作三角形两边的中垂线,两条中垂线的交点是圆心,圆心到顶点的距离是半径.
1.第一自然段主要说明
①圆的概念:此概念有2种解释
1)线段OA绕端点O旋转一周,另一个端点A随之旋转一周,所组成的图形叫圆.
2)到定点的距离等于定长的点的集合.
②圆心,半径,固定端点O叫圆心,OA的长叫半径.
作圆要两个条件:圆心确定圆的位置,圆心确定圆的大小.
③圆内部分:到定点(圆心)的距离小于定长(半径)的点的集合.
圆外部分:到定点(圆心)的距离大于定长(半径)的点的集合.
要确定一个点在圆上,圆外还是圆内,就要计算端点到圆心的距离,计算出距离与半径比较.若该距离d>r,则点在圆外,d=r,在圆上,d<r在圆内.
如⊙O的半径r=5cm,圆心O到直线l的距离d=OP=3cm.在l上有P,Q,R三点,且PD=4cm,QD>4cm,RD<4cm,则P,Q,R三点在⊙O的什么位置.
解:连结OP ∵PD=4cm OD=3cm
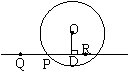 由勾股定理得:OP=5cm OP=r ∴P在⊙O上
由勾股定理得:OP=5cm OP=r ∴P在⊙O上
∵QD>4cm OD=3cm 连结OQ
则OQ2=OP2+QD2>25 ∴OQ>5cm ∴Q在⊙O外
用同样方法证得R在⊙O内.
 ④弦:连结圆上位意两点的线段,
④弦:连结圆上位意两点的线段,
如线段CD
经过圆心的弦叫直径
如AB(直径是圆的最大的弦)
⑤弧:圆上任意两点间的部分,弧若大于半圆叫优弧,小于半圆叫劣弧.

 ⑥弓形:由弦及其所对的弧组成的图形叫
⑥弓形:由弦及其所对的弧组成的图形叫
弓形.弦CD与弧CD及弦CD及优弧CD所有两个弓形.
⑦同心圆:圆心相同,半径不相等的两个圆叫同心圆.
 ⑧能够重合(或半径相等)的两个圆是等圆.
⑧能够重合(或半径相等)的两个圆是等圆.
⑨在同圆或等圆中,能够互相重合的弧叫等弧。
(注意:只要说两弧是等弧,就说明这两段弧在同圆或等圆上)
(二)证明题:
1.略 2.连结AB,BD,由射影定理得CD2=AC·CB,再证△BCF∽△APC.
3.(1)连结OD,则OD⊥DE,△OBD是等腰三角形,∠OBD=∠ODB=∠C,∴OD∥AC,∴OD⊥AC.
(2)由切割线定理得ED2=BE·EF,连结AD,由射影定理得DE2=AE·EC,∴AE·EC=BE·EF.
4.△ACP∽△BAP 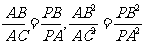
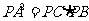 ∴
∴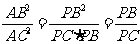
5.(1)△ACB和△CDB都Rt△ ∴∠CAD=∠BCD=∠EDB ∴DE∥AC
(2)△ACD∽△CDF 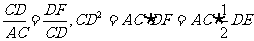 ∴
∴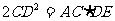 .
.
 6.(1)略 (2)设BP=
6.(1)略 (2)设BP=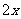 ,AP=
,AP=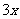 ,由割线定理得:
,由割线定理得: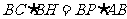 ∵BH=2BC∴2BC2=
∵BH=2BC∴2BC2=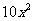
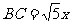 .由△ABH∽△AHP
.由△ABH∽△AHP 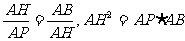
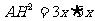 ∴
∴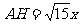 ∴
∴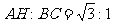
7.(1)(2)(3)略.(4)连结O,E交AB于F ∵∠1=∠2 ∴AE=BE,则O1E⊥AB,O1E平分AB ∴AB=2AF且∠AFE=Rt∠ △AEF≌△AEH AH=AF ∴AB=2AH
(5)∵∠FAE=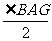 ∴
∴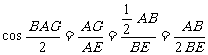
8.(1)略.(2)∵AE,BD是方程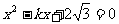 的根,AE+BD=
的根,AE+BD=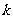 ,∠BED=∠A+∠APE,∠BDE=∠DAP+∠BPE ∴∠BDE=∠BED BD=BE
∴AE+BE=
,∠BED=∠A+∠APE,∠BDE=∠DAP+∠BPE ∴∠BDE=∠BED BD=BE
∴AE+BE=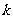 ∴AB=
∴AB=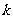 AB是直径.
AB是直径.
(3)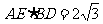 △ABP是Rt△,
△ABP是Rt△,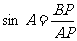 ∴
∴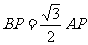 由(1)题结论
由(1)题结论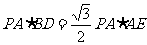 ∴
∴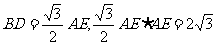 ∴
∴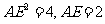 ,
,
BD=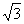
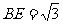
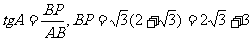
∴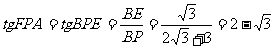
(一)填空题:
1.13 2.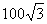 3.
3.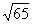 4.13cm 5.
4.13cm 5.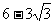 6.1或7cm 7.135°
6.1或7cm 7.135°
8.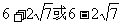 9.
9.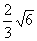 10.
10.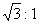 11.
11.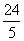 12.
12.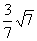 13.外离
13.外离
14.180° 15.R+r,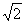 (R+r) 16.内切 17.
(R+r) 16.内切 17.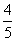 18.1 19.
18.1 19.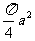
20.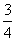 21.
21.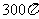 22.1 23.54
22.1 23.54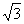
(二)证明题:
1.已知AB是⊙O的直径,AC是弦,直线CE切⊙O于C,AD⊥CE,垂足是D,
 求证:AC平分∠BAD.
求证:AC平分∠BAD.
B
O
A
E C D
2.已知AB是⊙O的直径,P是⊙O外一点,PC⊥AB于C,交⊙O于D,PA交⊙O于E,BE交PC于F点
 求证:CD2=CF·CP
P
求证:CD2=CF·CP
P
E D
F
A O C B
3.在△ABC中,AB=AC,以AB为直径做⊙O,交BC于D,过D点做⊙O的切线交AC于E,连结BE交⊙O于F
求证: (1)OE⊥AC;
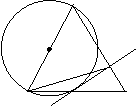 (2)AE·EC=BE·EF
A
(2)AE·EC=BE·EF
A
O
F E
B D C
4.已知PA是△ABC外接圆珠笔的切线,P是BC延长线上一点,
求证:PB:PC=AB2:AC2.
 A
P
A
P
C
B
5.已知AB是大圆直径,CE切⊙O于C,BC是小圆直径
求证:(1)DE∥AC;
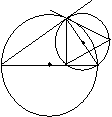 (2)DE·AC=2CD2;
C
(2)DE·AC=2CD2;
C
(3)DE=36,cosCDE=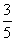 O’
E
O’
E
求⊙O的半径. A O D B
6.已知⊙O1和⊙O2外切于点P,BH切⊙O2于B,
|
 求证:(1)△BCP∽△HAP
H
求证:(1)△BCP∽△HAP
H
(2)若AP:PB=3:2,且C为 B
HB中点,求HA:BC的值.
O1 O2
A
7.如图: ⊙O和⊙O1,内切于P,PA,PB交 P
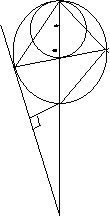 ⊙O1于A,B,AB切⊙O于D,AD交⊙O1 1
2
⊙O1于A,B,AB切⊙O于D,AD交⊙O1 1
2
于E,AG切⊙O1于A,AG,AD的延长线交于G, M O N
证明:(1)∠1=∠2; O1 D B
(2)PA·PB=PD·PE; A
(3)PA·PB=PD2+AD·BD; E
(4)AB=2AH; H
(5)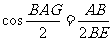 .
.
G
8.如图:AB是⊙O的直径,PB切⊙O B
 于B,PA交⊙O于C,∠APB的平分
于B,PA交⊙O于C,∠APB的平分
线分别交BC,AB于点D,E.交⊙O
于点F,∠A=60°且线段AE,BD 的长 F E D P
是方程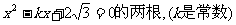 C
C
求证:(1)PA·BD=PB·AE; A
(2)⊙O的直径长为常数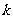 ;
;
(3)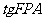 的值.
的值.
(一)填空题:
1.已知OC是半径,AB是弦,AB⊥OC于E,CE=1,AB=10,则OC=______.
2.AB是弦,OA=20cm,∠AOB=120°,则S△AOB=______.
3. 在⊙O中,弦AB,CD互相垂直于E,AE=2,EB=6,ED=3,EC=4,则⊙O的直径是______.
4.在⊙O中弦AB,CD互相平行,AB=24cm,CD=10cm,且AB与CD之间的距离是17cm,则⊙O的半径是______cm.
5.圆的半径是6cm,弦AB=6cm,则劣弧AB的中点到弦AB的中点的距离是______cm.
6.在⊙O中,半径长为5cm,AB∥CD,AB=6,CD=8,则AB,CD之间的距离是______cm.
7.圆内接四边形ABCD中,∠A:∠B:∠C=2:3:6,则四边形的最大角是______度.
8.在直径为12cm的圆中,两条直径AB,CD互相垂直,弦CE交AB于F,若CF=8cm,则AF的长是______cm.
9. 已知PA切⊙O于点A,PA=4cm,PCD是割线,PC=CD,若CD垂直平分半径OF,则⊙O的半径OF=______.
D F
已知PA切⊙O于点A,PA=4cm,PCD是割线,PC=CD,若CD垂直平分半径OF,则⊙O的半径OF=______.
D F
O C
P
A
10.已知CD切⊙O于D,割线CBA交⊙O于B,A,且CBA过O点,切线BE交CD于E点,若DE:EC=1:2,则AC:CD=______.
 E D
E D
C
B O
A
11.已知:AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,CD⊥AB于D,PB=4,AB=12,sin∠APC=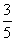 ,则CD=______.
,则CD=______.
12.已知PA,PB分别切⊙O于A,B两点,AC是⊙O的直径,PC交⊙O于D点,∠APB=60°AB=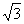 cm,则AC=______cm,PD=______cm.
cm,则AC=______cm,PD=______cm.
13.两圆半径分别是4,12,外公切线长是15,两圆的位置关系是______.
14.两圆相交于A,B,外公切线与两圆切于C,D,则∠CAD+∠CBD=______度.
15.两圆半径分别是R,r,(R>r)内公切线互相垂直,则内公切线长是______,圆心距是______.
16.两圆半径长是方程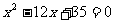 的两根,圆心距是2,则两圆的位置关系是______.
的两根,圆心距是2,则两圆的位置关系是______.
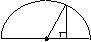
17.如图:PT切⊙O于T,PAB是过圆心O的割线,如果PT=4,PA=2,则cosBPT等于______.

O B
A
P
T
 18.已知CD是半圆的直径,AB⊥CD于B,设∠AOB=
18.已知CD是半圆的直径,AB⊥CD于B,设∠AOB=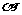 ,则
,则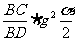 的值是______.
A
的值是______.
A
C O B D
19.正三角形的边长是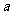 ,则内切圆与外接圆组成的环形面积是______.
,则内切圆与外接圆组成的环形面积是______.
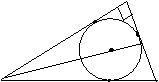
20.在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点是D,E,F.AD交BC交于G,若AC=3,CG=1,则⊙O的半径是______.
 C
C
D E
G
O
A F B
21.已知扇形的圆心角是120°,扇形弧长是20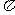 ,则扇形=______.
,则扇形=______.
22.边长是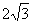 的正三角形的边心距是______.
的正三角形的边心距是______.
23.已知正六边形的半径是6,则该正六边形的面积是______.
(四)正多边形和圆
注意:公式的应用
1.已知R,求边长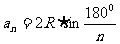 ,求边心距
,求边心距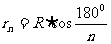
若已知边长,求边心距,可先利用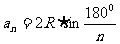 求出半径,再利用
求出半径,再利用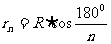 ,求边心距.
,求边心距.
如已知正三角形的边长是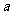 ,求边心距.
,求边心距.
解:∵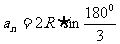 ∴
∴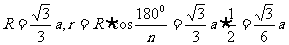
2.同圆的内接正n边形和外切正n边形的边长、半径、边心距、周长之比是cos .
.
如同圆内接正六边形和外切正六边形的面积之比是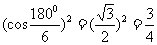 .
.
3.弧长公式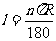
扇形面积公式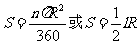
要求熟练应用公式,如怎样利用圆心角、半径求弧长或扇形面积,怎样利用弧长和圆心角求半径.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com