
2.下列运算正确的是
A.x2 + x3 = x5 B.(- x2 )3 = x6 C.x6÷x2 = x3 D.-2x·x2 =-2x3
1.-2的相反数是
A.-2 B.2 C.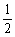 D.-
D.-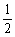
22.解:(1)①点M的坐标为(2,4),点F的坐标为(-2,8).……………………2分
②
 设
设 的函数解析式为
的函数解析式为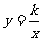 (
( .
.
∵ 过点F(-2,8)
过点F(-2,8)
∴ 的函数解析式为
的函数解析式为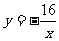 .
.
∵ 的顶点B的坐标是(0,6)
的顶点B的坐标是(0,6)
∴设 的函数解析式为
的函数解析式为 .
.
∵ 过点M(2,4)
过点M(2,4)
∴
 .
.
∴ 的函数解析式为
的函数解析式为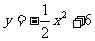 .……………………6分
.……………………6分
(2)依题意得,A(m,0),B(0,m),
∴点M坐标为(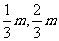 ),点F坐标为(
),点F坐标为(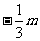 ,
, ).
).
①设 的函数解析式为
的函数解析式为 (
( .
.
∵ 过点F(
过点F(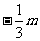 ,
, )
)
∴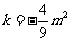 .
.
∵
∴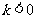
∴在 的每一支上,y随着x的增大而增大.
的每一支上,y随着x的增大而增大.
②答:当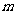 >0时,满足题意的x的取值范围为 0<x<
>0时,满足题意的x的取值范围为 0<x< ;
;
当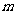 <0时,满足题意的x的取值范围为
<0时,满足题意的x的取值范围为 <x<0.
<x<0.
……………………………………………………14分
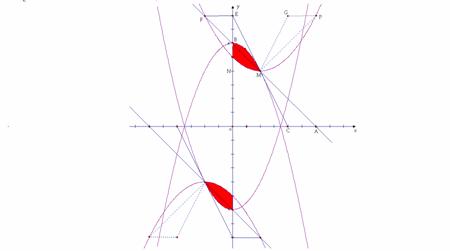
22.(满分14分)
如图10,已知直线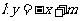 (
(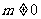 )交x轴、y轴于A、B两点,点C、M分别在线段OA、AB上,且OC=2CA,AM=2MB,连接MC,将△ACM绕点M旋转180°,得到△FEM,显然点E在y轴上, 点F在直线l上;取线段EO中点N,将△ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:过点F的反比例函数图象为
)交x轴、y轴于A、B两点,点C、M分别在线段OA、AB上,且OC=2CA,AM=2MB,连接MC,将△ACM绕点M旋转180°,得到△FEM,显然点E在y轴上, 点F在直线l上;取线段EO中点N,将△ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:过点F的反比例函数图象为 ,过点M且以B为顶点的二次函数图象为
,过点M且以B为顶点的二次函数图象为 ,过点P且以M为顶点的二次函数图象为
,过点P且以M为顶点的二次函数图象为 .全品中考网 全品 中考网
.全品中考网 全品 中考网
 (1)当m=6时,①直接写出点M、F的坐标,
(1)当m=6时,①直接写出点M、F的坐标,
②求 、
、 的函数解析式;
的函数解析式;
(2)当m发生变化时,
①在 的每一支上,y随x的增大如何变化?请说明理由.
的每一支上,y随x的增大如何变化?请说明理由.
②若 、
、 中的y都随着x的增大而减小,写出x的取值范围.
中的y都随着x的增大而减小,写出x的取值范围.
21.解:(1)BE、PE、BF三条线段中任选两条.………………………2分
 (2)在Rt△CHE中,∠CHE=90° ∠C=60°,
(2)在Rt△CHE中,∠CHE=90° ∠C=60°,
∴EH=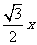
∵PQ=EF=BE=4-x
∴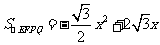 .……………………5分
.……………………5分
(3)

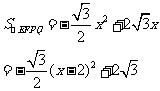
∴当x=2时,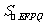 有最大值.
有最大值.
此时E、F、P分别为△ABC三边BC、AB、AC的中点,且点C、 点Q重合
∴平行四边形EFPQ是菱形.
过E点作ED⊥FP于D,
∴ED=EH=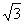 .
.
∴当⊙E与□EFPQ四条边交点的总个数是2个时,0<r<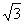 ;
;
当⊙E与□EFPQ四条边交点的总个数是4个时,r=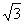 ;
;
当⊙E与□EFPQ四条边交点的总个数是6个时,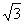 <r<2;
<r<2;
当⊙E与□EFPQ四条边交点的总个数是3个时,r=2时;
当⊙E与□EFPQ四条边交点的总个数是0个时,r>2时.
…………………………………………………………12分
易错分析:本题在分类中,容易把⊙E与□EFPQ四条边交点的总个数分不清楚,容易出现交点数多或少的漏洞.
21.(满分12分)
如图9,等边 边长为4,
边长为4, 是边
是边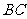 上动点,
上动点, 于H,过
于H,过 作
作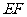 ∥
∥ ,交线段
,交线段 于点
于点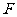 ,在线段
,在线段 上取点
上取点 ,使
,使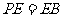 .设
.设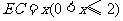 .
.
(1)请直接写出图中与线段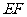 相等的两条线段(不再另外添加辅助线); 全品 中考网
相等的两条线段(不再另外添加辅助线); 全品 中考网
 (2)
(2) 是线段
是线段 上的动点,当四边形
上的动点,当四边形 是平行四边形时,求
是平行四边形时,求 的面积(用含
的面积(用含 的代数式表示);
的代数式表示);
(3)当(2)中 的 面积最大时,以E为圆心,
面积最大时,以E为圆心,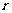 为半径作圆,根据⊙E与此时
为半径作圆,根据⊙E与此时 四条边交点的总个数,求相应
四条边交点的总个数,求相应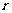 的取值范围.
的取值范围.
20. (每小题3分,共12分)
(每小题3分,共12分)
(1)如图
(2)
(3)∠CAD,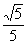 (或∠ADC,
(或∠ADC, )
)
(4)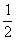
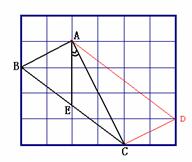
20.(满分12分)全品中考网 全品 中考网
如图8,在边长为1的小正方形组成的网格中, 的三个顶点均在格点上,
的三个顶点均在格点上,
请按要求完成下列各题:
(1)用签字笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在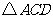 的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是
.
的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是
.
 (4)若E为BC中点,则tan∠CAE的值是
(4)若E为BC中点,则tan∠CAE的值是
19.(每小题各3分,共12分)
(1)50
(2)3
(3)普遍增加了
(4)15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com