
例2 填空:当a≥0时,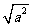 =_____;当a<0时,
=_____;当a<0时,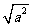 =_______,并根据这一性质回答下列问题.
=_______,并根据这一性质回答下列问题.
(1)若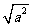 =a,则a可以是什么数?
=a,则a可以是什么数?
(2)若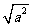 =-a,则a可以是什么数?
=-a,则a可以是什么数?
(3)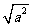 >a,则a可以是什么数?
>a,则a可以是什么数?
分析:∵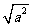 =a(a≥0),∴要填第一个空格可以根据这个结论,第二空格就不行,应变形,使“( )2”中的数是正数,因为,当a≤0时,
=a(a≥0),∴要填第一个空格可以根据这个结论,第二空格就不行,应变形,使“( )2”中的数是正数,因为,当a≤0时,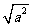 =
=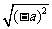 ,那么-a≥0.
,那么-a≥0.
(1)根据结论求条件;(2)根据第二个填空的分析,逆向思想;(3)根据(1)、(2)可知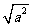 =│a│,而│a│要大于a,只有什么时候才能保证呢?a<0.
=│a│,而│a│要大于a,只有什么时候才能保证呢?a<0.
解:(1)因为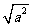 =a,所以a≥0;
=a,所以a≥0;
(2)因为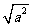 =-a,所以a≤0;
=-a,所以a≤0;
(3)因为当a≥0时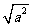 =a,要使
=a,要使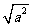 >a,即使a>a所以a不存在;当a<0时,
>a,即使a>a所以a不存在;当a<0时,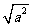 =-a,要使
=-a,要使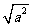 >a,即使-a>a,a<0综上,a<0
>a,即使-a>a,a<0综上,a<0
例3当x>2,化简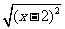 -
-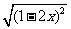 .
.
分析:(略)
教材P7练习2.
(学生活动)填空:
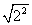 =_______;
=_______;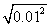 =_______;
=_______;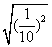 =______;
=______;
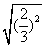 =________;
=________;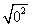 =________;
=________;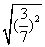 =_______.
=_______.
(老师点评):根据算术平方根的意义,我们可以得到:
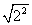 =2;
=2;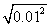 =0.01;
=0.01;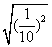 =
=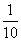 ;
;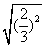 =
=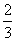 ;
;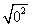 =0;
=0;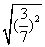 =
=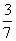 .
.
因此,一般地: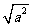 =a(a≥0)
=a(a≥0)
例1 化简
(1)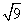 (2)
(2)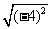 (3)
(3)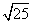 (4)
(4)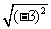
分析:因为(1)9=-32,(2)(-4)2=42,(3)25=52,
(4)(-3)2=32,所以都可运用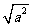 =a(a≥0)去化简.
=a(a≥0)去化简.
解:(1)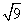 =
=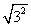 =3 (2)
=3 (2) =
=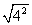 =4
=4
(3)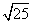 =
=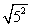 =5 (4)
=5 (4)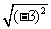 =
=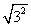 =3
=3
3.(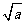 )2=a(a≥0).
)2=a(a≥0).
那么,我们猜想当a≥0时,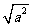 =a是否也成立呢?下面我们就来探究这个问题.
=a是否也成立呢?下面我们就来探究这个问题.
2.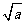 (a≥0)是一个非负数;
(a≥0)是一个非负数;
老师口述并板收上两节课的重要内容;
1.形如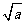 (a≥0)的式子叫做二次根式;
(a≥0)的式子叫做二次根式;
4.(1)x2-2=(x+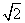 )(x-
)(x-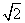 )
)
(2)x4-9=(x2+3)(x2-3)=(x2+3)(x+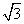 )(x-
)(x-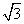 )
)
(3)略
课后教学反思:_______________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
________________________________________________________________________________________________________________________________________________________
3.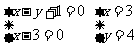 xy=34=81
xy=34=81
(4)(-3 )2=9×
)2=9×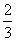 =6 (5)-6
=6 (5)-6
2.(1)5=(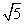 )2 (2)3.4=(
)2 (2)3.4=(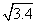 )2
)2
(3)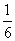 =(
=(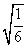 )2 (4)x=(
)2 (4)x=(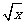 )2(x≥0)
)2(x≥0)
4.在实数范围内分解下列因式:
(1)x2-2 (2)x4-9 3x2-5
第二课时作业设计答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com