
本节课应掌握:
利用已学的特殊图形的面积公式建立一元二次方程的数学模型并运用它解决实际问题.
例3.如图(a)、(b)所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.
(1)如果P、Q分别从A、B同时出发,经过几秒钟,使S△PBQ=8cm2.
(2)如果P、Q分别从A、B同时出发,并且P到B后又继续在BC边上前进,Q到C后又继续在CA边上前进,经过几秒钟,使△PCQ的面积等于12.6cm2.(友情提示:过点Q作DQ⊥CB,垂足为D,则: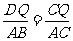 )
)
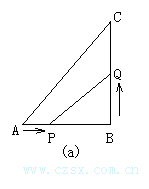
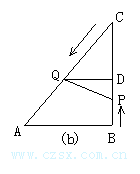
分析:(1)设经过x秒钟,使S△PBQ=8cm2,那么AP=x,PB=6-x,QB=2x,由面积公式便可得到一元二次方程的数学模型.
(2)设经过y秒钟,这里的y>6使△PCQ的面积等于12.6cm2.因为AB=6,BC=8,由勾股定理得:AC=10,又由于PA=y,CP=(14-y),CQ=(2y-8),又由友情提示,便可得到DQ,那么根据三角形的面积公式即可建模.
解:(1)设x秒,点P在AB上,点Q在BC上,且使△PBQ的面积为8cm2.
则: (6-x)·2x=8
(6-x)·2x=8
整理,得:x2-6x+8=0
解得:x1=2,x2=4
∴经过2秒,点P到离A点1×2=2cm处,点Q离B点2×2=4cm处,经过4秒,点P到离A点1×4=4cm处,点Q离B点2×4=8cm处,所以它们都符合要求.
(2)设y秒后点P移到BC上,且有CP=(14-y)cm,点Q在CA上移动,且使CQ=(2y-8)cm,过点Q作DQ⊥CB,垂足为D,则有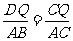
∵AB=6,BC=8
∴由勾股定理,得:AC=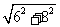 =10
=10
∴DQ=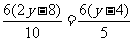
则: (14-y)·
(14-y)·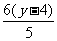 =12.6
=12.6
整理,得:y2-18y+77=0
解得:y1=7,y2=11
即经过7秒,点P在BC上距C点7cm处(CP=14-y=7),点Q在CA上距C点6cm处(CQ=2y-8=6),使△PCD的面积为12.6cm2.
经过11秒,点P在BC上距C点3cm处,点Q在CA上距C点14cm>10,
∴点Q已超过CA的范围,即此解不存在.
∴本小题只有一解y1=7.
有一张长方形的桌子,长6尺,宽3尺,有一块台布的面积是桌面面积的2倍,并且铺在桌面上时,各边垂下的长度相同,求台布的长和宽各是多少?(精确到0.1尺)
现在,我们根据刚才所复习的面积公式来建立一些数学模型,解决一些实际问题.
例1.某林场计划修一条长750m,断面为等腰梯形的渠道,断面面积为1.6m2,上口宽比渠深多2m,渠底比渠深多0.4m.
(1)渠道的上口宽与渠底宽各是多少?
(2)如果计划每天挖土48m3,需要多少天才能把这条渠道挖完?
分析:因为渠深最小,为了便于计算,不妨设渠深为xm,则上口宽为x+2,渠底为x+0.4,那么,根据梯形的面积公式便可建模.
解:(1)设渠深为xm
则渠底为(x+0.4)m,上口宽为(x+2)m
依题意,得: (x+2+x+0.4)x=1.6
(x+2+x+0.4)x=1.6
整理,得:5x2+6x-8=0
解得:x1=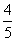 =0.8m,x2=-2(舍)
=0.8m,x2=-2(舍)
∴上口宽为2.8m,渠底为1.2m.
(2)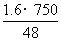 =25天
=25天
答:渠道的上口宽与渠底深各是2.8m和1.2m;需要25天才能挖完渠道.
学生活动:例2.如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?

老师点评:依据题意知:中央矩形的长宽之比等于封面的长宽之比=9:7,由此可以判定:上下边衬宽与左右边衬宽之比为9:7,设上、下边衬的宽均为9xcm,则左、右边衬的宽均为7xcm,依题意,得:中央矩形的长为(27-18x)cm,宽为(21-14x)cm.
因为四周的彩色边衬所点面积是封面面积的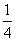 ,则中央矩形的面积是封面面积的.
,则中央矩形的面积是封面面积的.
所以(27-18x)(21-14x)=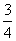 ×27×21
×27×21
整理,得:16x2-48x+9=0
解方程,得:x=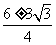 ,
,
x1≈2.8cm,x2≈0.2
所以:9x1=25.2cm(舍去),9x2=1.8cm,7x2=1.4cm
因此,上下边衬的宽均为1.8cm,左、右边衬的宽均为1.4cm.
6.圆的面积公式是什么?
(学生口答,老师点评)
5.平行四边形的面积公式是什么?
4.菱形的面积公式是什么?
3.梯形的面积公式是什么?
(口述)1.直角三角形的面积公式是什么?一般三角形的面积公式是什么呢?
2.正方形的面积公式是什么呢?长方形的面积公式又是什么?
3.某玩具厂有4个车间,某周是质量检查周,现每个车间都原有a(a>0)个成品,且每个车间每天都生产b(b>0)个成品,质量科派出若干名检验员周一、周二检验其中两个车间原有的和这两天生产的所有成品,然后,周三到周五检验另外两个车间原有的和本周生产的所有成品,假定每名检验员每天检验的成品数相同.
(1)这若干名检验员1天共检验多少个成品?(用含a、b的代数式表示)
(2)若一名检验员1天能检验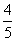 b个成品,则质量科至少要派出多少名检验员?
b个成品,则质量科至少要派出多少名检验员?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com