
2.选作课时作业设计.
第一课时作业设计
1.教材P21 习题21.3 1、2、3、5.
本节课应掌握:(1)不是最简二次根式的,应化成最简二次根式;(2)相同的最简二次根式进行合并.
例3.已知4x2+y2-4x-6y+10=0,求(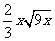 +y2
+y2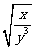 )-(x2
)-(x2 -5x
-5x )的值.
)的值.
分析:本题首先将已知等式进行变形,把它配成完全平方式,得(2x-1)2+(y-3)2=0,即x=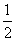 ,y=3.其次,根据二次根式的加减运算,先把各项化成最简二次根式,再合并同类二次根式,最后代入求值.
,y=3.其次,根据二次根式的加减运算,先把各项化成最简二次根式,再合并同类二次根式,最后代入求值.
解:∵4x2+y2-4x-6y+10=0 ∴4x2-4x+1+y2-6y+9=0
∴(2x-1)2+(y-3)2=0 ∴x=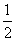 ,y=3
,y=3
原式=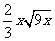 +y2
+y2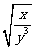 -x2
-x2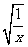 +5x
+5x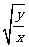
=2x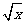 +
+ -x
-x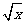 +5
+5 =x
=x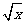 +6
+6
当x=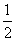 ,y=3时,原式=
,y=3时,原式=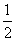 ×
×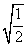 +6
+6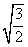 =
=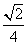 +3
+3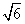
教材P19 练习1、2.
学生活动:计算下列各式.
(1)2 +3
+3 (2)2
(2)2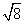 -3
-3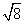 +5
+5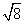
(3)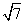 +2
+2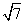 +3
+3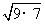 (4)3
(4)3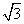 -2
-2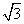 +
+
老师点评:
(1)如果我们把 当成x,不就转化为上面的问题吗?
当成x,不就转化为上面的问题吗?
2 +3
+3 =(2+3)
=(2+3) =5
=5
(2)把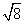 当成y;
当成y;
2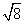 -3
-3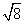 +5
+5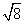 =(2-3+5)
=(2-3+5)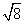 =4
=4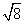 =8
=8
(3)把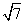 当成z;
当成z;
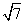 +2
+2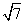 +
+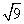
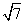 =2
=2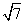 +2
+2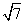 +3
+3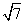 =(1+2+3)
=(1+2+3)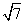 =6
=6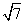
(4)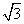 看为x,
看为x, 看为y.
看为y.
3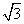 -2
-2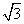 +
+ =(3-2)
=(3-2)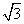 +
+ =
=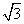 +
+
因此,二次根式的被开方数相同是可以合并的,如2 与
与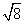 表面上看是不相同的,但它们可以合并吗?可以的.
表面上看是不相同的,但它们可以合并吗?可以的.
(板书)3 +
+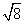 =3
=3 +2
+2 =5
=5
3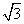 +
+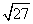 =3
=3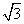 +3
+3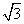 =6
=6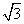
所以,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
例1.计算
(1)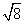 +
+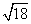 (2)
(2)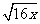 +
+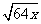
分析:第一步,将不是最简二次根式的项化为最简二次根式;第二步,将相同的最简二次根式进行合并.
解:(1)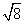 +
+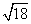 =2
=2 +3
+3 =(2+3)
=(2+3) =5
=5
(2)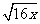 +
+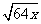 =4
=4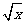 +8
+8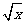 =(4+8)
=(4+8)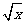 =12
=12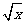
例2.计算
(1)3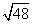 -9
-9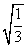 +3
+3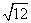 (2)(
(2)(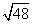 +
+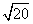 )+(
)+(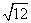 -
-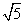 )
)
解:(1)3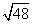 -9
-9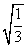 +3
+3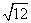 =12
=12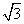 -3
-3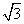 +6
+6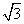 =(12-3+6)
=(12-3+6)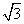 =15
=15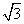
(2)(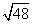 +
+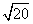 )+(
)+(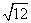 -
-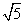 )=
)=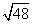 +
+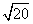 +
+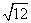 -
-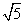
=4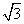 +2
+2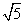 +2
+2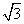 -
-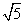 =6
=6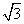 +
+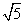
学生活动:计算下列各式.
(1)2x+3x; (2)2x2-3x2+5x2; (3)x+2x+3y; (4)3a2-2a2+a3
教师点评:上面题目的结果,实际上是我们以前所学的同类项合并.同类项合并就是字母不变,系数相加减.
26.解:原式=(2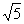 +1)(
+1)(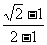 +
+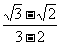 +
+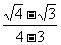 +…+
+…+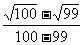 )
)
=(2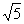 +1)[(
+1)[(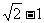 )+(
)+(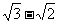 )+(
)+(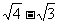 )+…+(
)+…+(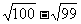 )]
)]
=(2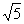 +1)(
+1)(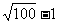 )
)
=9(2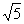 +1).
+1).
25. 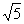
答案:解:(1)所画⊙P如图所示,由图可知⊙P的半径为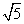 ,而
,而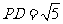 .
.
 点
点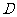 在⊙P上.
在⊙P上.
(2)① 直线
直线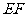 向上平移1个单位经过点
向上平移1个单位经过点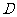 ,
,
且经过点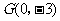 ,
,
 ,
,
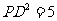 ,
,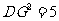 .
.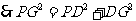 .
.
则 ,
, .
. 直线
直线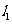 与⊙P相切.
与⊙P相切.
②
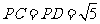 ,
,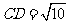 ,
,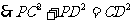 .
.
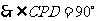 .
.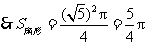 ,
,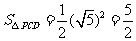 .
.
24.解:(菱形的边长)2=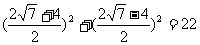
∴菱形的边长=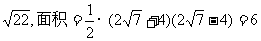
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com