
问题 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系
h=20t-5t2.
考虑以下问题
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?
分析:由于球的飞行高度h与飞行时间t的关系是二次函数
h=20t-5t2.
所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程,如果方程有合乎实际的解,则说明球的飞行高度可以达到问题中h的值:否则,说明球的飞行高度不能达到问题中h的值.
解:(1)解方程 15=20t-5t2. t2-4t+3=0. t1=1,t2=3.
当球飞行1s和3s时,它的高度为15m.
(2)解方程 20=20t-5t2. t2-4t+4=0. t1=t2=2.
当球飞行2s时,它的高度为20m.
(3)解方程 20.5=20t-5t2. t2-4t+4.1=0.
因为(-4)2-4×4.1<0.所以方程无解.球的飞行高度达不到20.5m.
(4)解方程 0=20t-5t2. t2-4t=0. t1=0,t2=4.
当球飞行0s和4s时,它的高度为0m,即0s时球从地面飞出.4s时球落回地面.
播放课件:函数的图像,画出二次函数h=20t-5t2的图象,观察图象,体会以上问题的答案.
从上面可以看出.二次函数与一元二次方程关系密切.
由学生小组讨论,总结出二次函数与一元二次方程的解有什么关系?
例如:已知二次函数y=-x2+4x的值为3.求自变量x的值.可以解一元二次方程-x2+4x=3(即x2-4x+3=0) .反过来,解方程x2-4x+3=0又可以看作已知二次函数y=x2-4+3的值为0,求自变量x的值.
一般地,我们可以利用二次函数y=ax2+bx+c深入讨论一元二次方程ax2+bx+c=0.
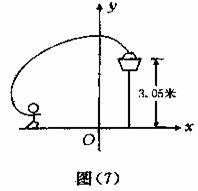
4.如图(7),一位篮球运动员跳起投篮,球沿抛物线y=-x2+3.5运行,然后准确落人篮框内。已知篮框的中心离地面的距离为3.05米。
(1)球在空中运行的最大高度为多少米?
(2)如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?
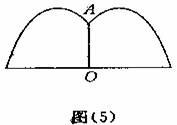
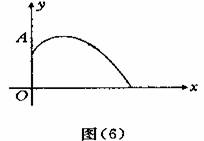
3.学校建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA。O恰好在水面中心,布置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA任意平面上的抛物线如图(5)所示,建立直角坐标系(如图(6)),水流喷出的高度y(m)与水面距离x(m)之间的函数关系式是y=-x2+x+,请回答下列问题:
(1)花形柱子OA的高度;
(2)若不计其他因素,水池的半径至少要多少米,才能使喷出的水不至于落在池外?
2.已知函数y=x2-x-2。
(1)先确定其图象的开口方向、对称轴和顶点坐标,再画出图象
(2)观察图象确定:x取什么值时,①y=0,②y>0;③y<0。
1. 二次函数y=x2-3x-18的图象与x轴有两交点,求两交点间的距离。
2.若二次函数y=ax2+bx+c的图象与x轴无交点,试说明,元二次方程ax2+bx+c=0和一元二次不等式ax2+bx+c>0、ax2+bx+c<0的解的情况。
根据问题3的图象回答下列问题。
(1)当x取何值时,y<0?当x取何值时,y>0?
(当-<x<时,y<0;当x<-或x>时,y>0)
(2)能否用含有x的不等式来描述(1)中的问题? (能用含有x的不等式采描述(1)中的问题,即x2-x-<0的解集是什么?x2-x->0的解集是什么?)
想一想:二次函数与一元二次不等式有什么关系?
让学生类比二次函数与一元二次不等式方程的关系,讨论、交流,达成共识:
(1)从“形”的方面看,二次函数y=ax2+bJ+c在x轴上方的图象上的点的横坐标,即为一元二次不等式ax2+bx+c>0的解;在x轴下方的图象上的点的横坐标.即为一元二次不等式ax2+bx+c<0的解。
(2)从“数”的方面看,当二次函数y=ax2+bx+c的函数值大于0时,相应的自变量的值即为一元二次不等式ax2+bx+c>0的解;当二次函数y=ax2+bx+c的函数值小于0时,相应的自变量的值即为一元二次不等式ax2+bc+c<0的解。这一结论反映了二次函数与一元二次不等式的关系。
6.对于问题(3),教师组织学生分组讨论、交流,各组选派代表发表意见,全班交流,达成共识:从“形”的方面看,函数y=x2-x-的图象与x轴交点的横坐标,即为方程x2-x-=0的解;从“数”的方面看,当二次函数y=x2-x-的函数值为0时,相应的自变量的值即为方程x2-x-=0的解。更一般地,函数y=ax2+bx+c的图象与x轴交点的横坐标即为方程ax2+bx+c=0的解;当二次函数y=ax2+bx+c的函数值为0时,相应的自变量的值即为方程ax2+bx+c=0的解,这一结论反映了二次函数与一元二次方程的关系。
5.让学生完成(2)的解答。教师巡视指导并讲评。
4.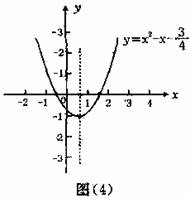 教师引导学生观察函数图象,回答(1)提出的问题,得到图象与x轴交点的坐标分别是(-,0)和(,0)。
教师引导学生观察函数图象,回答(1)提出的问题,得到图象与x轴交点的坐标分别是(-,0)和(,0)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com