
1.通过由学生动手操作:用各种不同长度的木棒去拼三角形,归纳出能拼出三角形的各边长之间的关系和不能拼成三角形的三边的特征,目的是归纳出同时符合几不同条件的不等式的公共范围,即不等式组的解集.毛
2、比一比看准反应快
|
|
①{ ②{
|
|
|
|
|
问题与情境 |
师生行为 |
设计意图 |
|
活动4 ①这节课对你来说有哪些收获?谈谈你的体会。 ②通过这节课,你学会了哪些思考问题的方法? ③你的遗憾是…… |
教师提出问题。 学生小结,谈感想 教师关注学生情感的变化 |
通过开放式问题小结,帮助学生自主回顾,总结梳理所学知识,既注重知识技能小结,又注重情感态度的形成。 |
|
活动5 1 必做题 P147页 T1、2 2 讨论题 P148页 T7、8 3 课外思考:有两根木条a和b,a长10cm,b长3cm,现要再找一根木条c,用这三根木条钉成一个三角形木框,若三角形的周长是偶数,则木条c的长可以是多少? |
教师布置作业 学生独立完成 |
课堂早已不再是知识获取的唯一途径,让学习在课堂之外延续,让新知在课后延伸.我特设计三个层次的作业:一是旨在巩固双基。二是旨在让不同的人学习不同的数学。 |
1、解下列不等式组
|
|
|
③{
(三)探究拓展
6.已知不等式组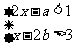 的解集为-1<x<1,则(a+1)(b-1)的值等于多少?
的解集为-1<x<1,则(a+1)(b-1)的值等于多少?
(二)创新提升
5.是否存在实数x,使得x+3<5,且x+2>4.
(一)双基练习
1.解不等式组: 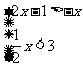
2.解不等式组: 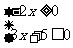
3.解不等式组: 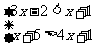
4.解不等式组: 
(三)归纳总结,知识回顾
1.你是如何确定方程组的解的?
方程组的解即是指同时满足各个方程的解.
2.方程组的解与不等式组的解有什么异同?
无论是方程组还是不等式组,它们的解均是指同时满足各个方程(不等式)的解的公共部分,但方程组的解一般只有一组,而不等式组的解一般有很多范围可选择.
3.不等式组的解的四种情形.
作业设计
(二)导入知识,解释疑难
1.教材内容讲解
通过以上分析可知一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集,解不等式组就是求它的解集.
例:解下列不等式组,并把解集在数轴上表示出来.
(1) 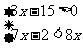 (2)
(2)
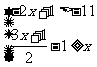
(3) 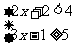 (4)
(4)
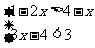
解:(1)由①得x>5,由②得x>-2,在数轴上表示为如图.
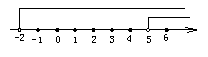
它们的公共部分为x>5,故不等式组的解集为x>5.
(2)由不等式①得x<6,由不等式②得x≥1,在数轴上表示为如图.
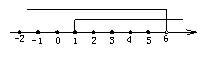
它们的公共部分为1≤x<6,即为不等式组的解集.
(3)由不等式①得x<1,由不等式②得x≥2,在数轴上表示为如图.
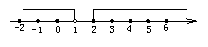
它们没有公共部分,故此不等式组无解.
(4)由不等式①得x<-3,由不等式②得x<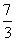 ,在数轴上表示为如图.
,在数轴上表示为如图.
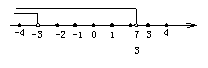
它们的公共部分是x<-3,即为不等式组的解集.
由上述四例可发现不等式组的解集有四种情况:
若a>b:①当 时,则不等式的公共解集为x>a;
时,则不等式的公共解集为x>a;
②当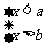 时,不等式的公共解集为b<x<a;
时,不等式的公共解集为b<x<a;
③当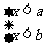 时,不等式的公共解集为x<b;
时,不等式的公共解集为x<b;
④当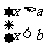 时,不等式组无解.
时,不等式组无解.
练习:解下列不等式组:
(1)  (2)
(2) 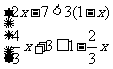 (3)
(3) 
解:(1)不等式2x+5≤3(x+2)的解为x≥-1,不等式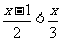 的解为x<3,故不等式组的解集为-1≤x<3.
的解为x<3,故不等式组的解集为-1≤x<3.
(2)不等式2x-7<3(1-x)的解为x<2,不等式 的解为x≤-1,故不等式组的公共解集为x≤-1.
的解为x≤-1,故不等式组的公共解集为x≤-1.
(3)不等式5x+3>8x-2的解为x<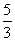 ,不等式
,不等式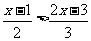 的解为x<3,故不等式组的公共解集为x<
的解为x<3,故不等式组的公共解集为x<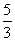 .
.
2.探究活动
试确定以下不等式组的解集:
(1)求不等式组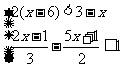 的整数解.
的整数解.
(2)解不等式组 (3)
(3) 
解:(1)2(x-6)<3-x的解集为x<5, 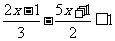 的解集为x≥-1.不等式组的公共解集为-1≤x<5,其整数解有-1,0,1,2,3,4,故不等式组的整数解为-1,0,1,2,3,4.
的解集为x≥-1.不等式组的公共解集为-1≤x<5,其整数解有-1,0,1,2,3,4,故不等式组的整数解为-1,0,1,2,3,4.
(2)不等式2x-5<3x+4的解集为x>-9,不等式4(3x-1)<5(2x+1)的解集为x<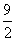 ,不等式
,不等式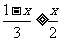 的解集为x≤
的解集为x≤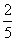 ,不等式组的公共解集必须同时满足这三个不等式,故其解集为-9<x≤
,不等式组的公共解集必须同时满足这三个不等式,故其解集为-9<x≤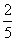 .
.
(3)x-7<0的解集为x<7,x-5<0的解集为x<5,x+3>0的解集为x>-3,x+1>0的解集为x>-1,不等式组的解集必须同时满足这四个不等式,故其公共解集为-1<x<5.
(一)提出问题,引发讨论
在学习不等式组之前,我们来开展小组活动吧,每个小组的同学准备五根小木棒,使它们的长度依次为3cm、10cm、6cm、9cm和14cm,用这些小木棒来搭三角形,要求所搭成的三角形的三边中必须有3cm和10cm这两根木棒,请大家先想想我们还有多少种不同的搭配方式,它们都能搭出三角形吗?再动手试试,验证你们的想法.
搭配方式有三种:3cm、10cm、6cm;3cm、10cm、9cm;3cm、10cm、14cm.但并不是每种搭配方式都能搭成三角形.要构成三角形,必须有两条较短的边拼起来后要略比长边长,也即“任意两边之和大于第三边”,将此不等式变形后成为“任意两边之差小于第三边”,这样可发现只有一种搭配方式可构成三角形,通过拼图验证可得到如课本P143中图.

用不等式来解释,设第三边长为xcm,则有x>10-3又x<10+3,即x>7与x<13,这二者并不矛盾,比7大比13小的数在数轴上可表示为如图9.3-1-1的阴影部分,在这部分数中任取一个都能与10cm和3cm构成一个三角形,所给的三条边6cm、9cm、14cm中只有9cm符合要求.这就是说第三边的取值必须同时满足两个条件:比7大且比13小,把x>7与x<13组合成一个整体即构成一元一次不等式组,即把两个不等式合起来,组成一个一元一次不等式组.由此例可知不等式组的解集即为各个不等式的解集的公共部分.
冬天到了,天气渐渐变冷,同学们在上学的路上未免会感觉到寒意,尤其是骑自行车上学的同学更觉得冷,妈妈们为了他们的孩子能过得舒服一些,都会给他们的孩子准备好帽子、手套来御寒.就拿手套来说吧,贵的可达几十元钱一双,便宜的呢,只要一、二元就可买到,但其质量和保暖程度肯定不相同,便宜的可能用的时间不长,而贵的对小孩来说不善于保护,又未免太奢侈了,作为家长肯定希望所买的东西价廉又物美,假设妈妈的要求是手套的价格不能超过6元,而小孩又不喜欢太便宜的,他们对家长的要求是所买的手套价格不能少于4元,同学们,如果你是商店售货员,你会拿什么价格的手套给他们选择呢?如果商店里的手套从每双2.5元至16元的各种价格都有,且每双不同的手套之间都是按逐渐提高0.5元的价格进行呈列的,你能确定他们的选择有几种吗?
当然可以,太简单了,要使买的手套让家长和小孩都满意可让他们从每双4元至6元的这些物品中选,由于这档手套有4元/双,4.5元/双,5元/双,5.5元/双,6元/双共五种,故售货员只需从这五种价格的手套中取出供他们挑选,就能让母子同时满意.这里我们所用到的数学知识就是:如何确定不等式组的公共解集.今天我们就共同来探讨不等式组吧.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com