3、渗透图形的外在美和内在关系．

　教学重点：简单组合图形的分解．

　教学难点：对图形的分解和组合．

　教学活动设计：

2、进一步培养学生的观察能力、发散思维能力和综合运用知识分析问题、解决问题的能力；

圆、扇形、弓形的面积(三)

　教学目标：

1、掌握简单组合图形分解和面积的求法；

3、分解简单组合图形为规则圆形的和与差．

2、应用弓形面积解决实际问题；

1、弓形面积的计算：首先看弓形弧是半圆、优弧还是劣弧，从而选择分解方案；

　练习：

　(1)如果弓形的弧所对的圆心角为60°，弓形的弦长为a，那么这个弓形的面积等于_______；

　(2)如果弓形的弧所对的圆心角为300°，弓形的弦长为a，那么这个弓形的面积等于_______．

　(学生独立完成，巩固新知识)

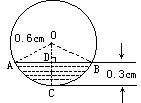
　例3、水平放着的圆柱形排水管的截面半径是0.6m，其中水面高是0.3m．求截面上有水的弓形的面积．(精确到0.01m²)

　 教师引导学生并渗透数学建模思想，分析：

　(1)“水平放着的圆柱形排水管的截面半径是0.6m”为你提供了什么数学信息？

　(2)求截面上有水的弓形的面积为你提供什么信息？

　(3)扇形、三角形、弓形是什么关系，选择什么公式计算？

　学生完成解题过程，并归纳三角形OAB的面积的求解方法．

　 反思：①要注重题目的信息，处理信息；②归纳三角形OAB的面积的求解方法，根据条件特征，灵活应用公式；③弓形的面积可以选用图形分解法，将它转化为扇形与三角形的和或差来解决．

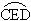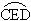　例4、已知：⊙O的半径为R，直径AB⊥CD，以B为圆心，以BC为半径作 ．求 与 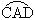围成的新月牙形ACED的面积S．

　解：∵ ，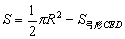

　有∵ ，

　 ， ，

　∴ ．

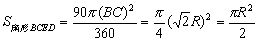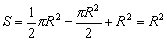　组织学生反思解题方法：图形的分解与组合；公式的灵活应用．

　提出问题：怎样求弓形的面积呢？

　学生以小组的形式研究，交流归纳出结论：

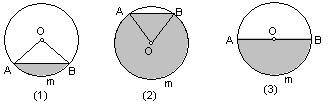
　(1)当弓形的弧小于半圆时，弓形的面积等于扇形面积与三角形面积的差；

　(2)当弓形的弧大于半圆时，它的面积等于扇形面积与三角的面积的和；

　(3)当弓形弧是半圆时，它的面积是圆面积的一半．

　理解：如果组成弓形的弧是半圆，则此弓形面积是圆面积的一半；如果组成弓形的弧是劣弧则它的面积等于以此劣弧为弧的扇形面积减去三角形的面积；如果组成弓形的弧是优弧，则它的面积等于以此优弧为弧的扇形面积加上三角形的面积．也就是说：要计算弓形的面积，首先观察它的弧属于半圆？劣弧？优弧？只有对它分解正确才能保证计算结果的正确．

　弓形：由弦及其所对的弧组成的图形叫做弓形．

　弦AB把圆分成两部分，这两部分都是弓形．弓形是一个最简单的组合图形之一．

3、通过面积问题实际应用题的解决，向学生渗透理论联系实际的观点．

　教学重点：扇形面积公式的导出及应用．

　教学难点：对图形的分解和组合、实际问题数学模型的建立．

　教学活动设计：