8. 已知点A(1, 3)，则点A关于x轴对称的点的坐标是________，点A关于y轴对称的点的坐标是________，点A关于原点对称的点的坐标是_________．

7. 点P(a , b)关于x轴、y轴的对称点的坐标分别为_________、_________．

6. 一个正方形的边长为7cm,它的边长减少xcm后得的新正方形的周长为ycm,则y与x之间的函数关系式为_______,自变量取值范围是________.

5.

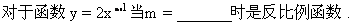
4.

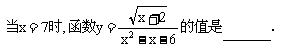
3.

2. 若点P的坐标是(a , b)，当a=0，b>0时，P点的位置在__________．

1. 函数y=kx+3的图象不经过第三象限则k_____0．(填><=号)

　(1)用量角器等分圆周作正n边形；

　(2)用尺规作正方形及由此扩展作正八边形、用尺规作正六边形及由此扩展作正12边形、正三角形．

1、用量角器等分圆：

　依据：等圆中相等的圆心角所对应的弧相等．

　操作：两种情况：其一是依次画出相等的圆心角来等分圆，这种方法比较准确，但是麻烦；其二是先用量角器画一个圆心角，然后在圆上依次截取等于该圆心角所对弧的等弧，于是得到圆的等分点，这种方法比较方便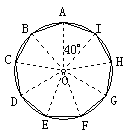，但画图的误差积累到最后一个等分点，使画出的正多边形的边长误差较大．

　问题2：把半径为2cm⊙O九等份．

　(先画半径2cm的圆，然后把360°的圆心角9等份，每一份40°)

　归纳：用量角器等分圆，方法简便，可以把圆任意n等分，但有误差．

　2、用尺规等分圆：

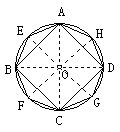
　(1)问题3：作正四边形、正八边形．

　教师组织学生，分析、作图．

　归纳：只要作出已知⊙O的互相垂直的直径即得圆内接正方形，再过圆心作各边的垂线与⊙O相交，或作各中心角的角平分线与⊙O相交，即得圆接正八边形，照此方法依次可作正十六边形、正三十二边形、正六十四边形……

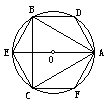　(2)问题4：作正六、三、十二边形．

　教师组织学生，分析、作图．

　归纳：先作出正六边形，则可作正三角形，正十二边形，正二十四边形………理论上我们可以一直画下去，但大家不难发现，随着边数的增加，正多边形越来越接近于圆，正多边形将越来越难画．