
27、解: BD=AD=300 (1′) CD=100,BC=200 (3′)
1号救生员:100÷6+300÷2≈178.9 (5′)
2号救生员:200÷2≈173.2 (7′)
26、解:(1)证得△PCD∽△PAB (3′)
(2) 由相似得= (4′)
由圆周角定理得∠ADB=90° (5′)
=cos60°=1/2 (6′)
∴=1/2 (7′)
25、设道路宽为xm,(32-x)(20-x)=540 (3′)
x1=50(舍去),x2=2 (5′)
答:道路宽为2m。 (6′)
24、略(每个三角形各2分)
23、解:∵△ABC,△DEF为等边三角形。
∴∠B=∠C=∠DEF=60° (1′)
∴∠BED+∠FEC=120°
又∠FEC+∠EHC=120°
∴∠BED=∠EHC (3′)
∴△DBE∽△ECH (5′)
22、(1)原式=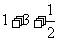 (2′)
(2) 原式=2-1+2+2 +1 (2′)
(2′)
(2) 原式=2-1+2+2 +1 (2′)
=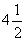 (4′)
=4+2 (4′)
(4′)
=4+2 (4′)
(3)解:x1=0,x2=5 (4′)
(3)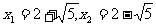 (4′)
(4′)
29、解:(1)∵∠B1CE=∠B1A1O=90°,∠CB1M=∠OB1A
∴△B1CM∽△B1A1O (1′)
(2)B1(0,5),B1C=1 (3′)
图2中,同理△B2CM1∽△B2A2P
∴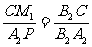 即
即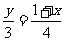
∴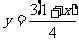 , 当
, 当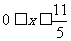 时,
时,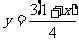 (5′)
(5′)
图3中, 当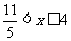 时,
时,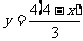 (7′)
(7′)
(3)图2中,S=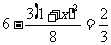 ,不成立,舍去。(9′)
,不成立,舍去。(9′)
图3中,S=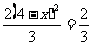 ,x=3 (11′)
,x=3 (11′)
28、解:(1)P6(0,-64).··················································································· 2分
(2)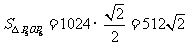 ······································································ 4分
······································································ 4分
(3)由题意知,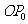 旋转
旋转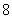 次之后回到
次之后回到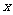 轴正半轴,在这
轴正半轴,在这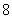 次中,点
次中,点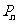 分别落在坐标象限的平分线上或
分别落在坐标象限的平分线上或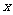 轴或
轴或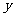 轴上,但各点绝对坐标的横、纵坐标均为非负数,因此,点
轴上,但各点绝对坐标的横、纵坐标均为非负数,因此,点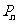 的坐标可分三类情况:
的坐标可分三类情况:
令旋转次数为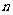
①当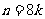 或
或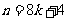 时(其中
时(其中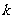 为自然数),或当点
为自然数),或当点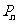 落在
落在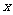 轴上,
轴上,
此时,点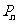 的绝对坐标为
的绝对坐标为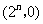 ;········································································· 6分
;········································································· 6分
②当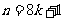 或
或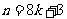 或
或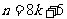 或
或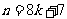 时(其中
时(其中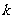 为自然数),或当点
为自然数),或当点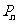 落在各象限的平分线上,
落在各象限的平分线上,
此时,点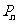 的绝对坐标为
的绝对坐标为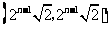 ···························································· 8分
···························································· 8分
③当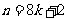 或
或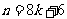 时(其中
时(其中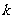 为自然数),或当点
为自然数),或当点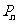 落在
落在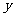 轴上,
轴上,
此时,点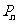 的绝对坐标为
的绝对坐标为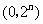 .······································································· 10分
.······································································· 10分
178.9﹥173.2, 2号救生员先到达B点。 (8′)
27、解: BD=AD=300 (1′)
CD=100,BC=200 (3′)
1号救生员:100÷6+300÷2≈178.9 (5′)
2号救生员:200÷2≈173.2 (7′)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com