
18、(2006河北)图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部截面的示意图, 所在圆的圆心为O.
所在圆的圆心为O.

 车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留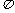 ).
).
解:连结OB,过点O作OE⊥AB,垂足为E,交 于F,如图1.
于F,如图1.
 由垂径定理,可知: E是AB中点,F是
由垂径定理,可知: E是AB中点,F是 中点,
中点,
∴EF是弓形高 .
∴AE=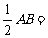 2
2 ,EF=2.
,EF=2.
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理,得 R 2= .
.
解得 R =4.
∵sin∠AOE= , ∴ ∠AOE=60°,
, ∴ ∠AOE=60°,
∴∠AOB=120°. ∴  的长为
的长为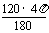 =
=
 .
.
∴帆布的面积为
 ×60=160
×60=160 (平方米).
(平方米).
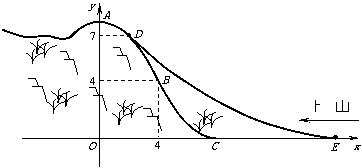
17、(2006浙江嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为 ,且已知
,且已知 .
.
(1)设 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处, (米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为
(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为 .试求索道的最大悬空高度.
.试求索道的最大悬空高度.

解:(1)∵ 是山坡线AB上任意一点,
是山坡线AB上任意一点,
∴ ,
,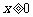 ,
,
∴ ,
,
∵ ,∴
,∴ =4,∴
=4,∴
(2)在山坡线AB上, ,
,
①令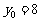 ,得
,得 ;令
;令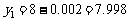 ,得
,得
∴第一级台阶的长度为 (百米)
(百米) (厘米)
(厘米)
同理,令 、
、 ,可得
,可得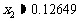 、
、
∴第二级台阶的长度为 (百米)
(百米) (厘米)
(厘米)
第三级台阶的长度为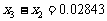 (百米)
(百米) (厘米)
(厘米)
②取点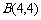 ,又取
,又取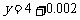 ,则
,则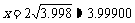
∵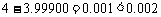
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴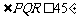
当其中有一级台阶的长大于它的高时,
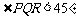 (…9分)
(…9分)
在题设图中,作 于H
于H
则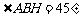 ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚 (…10分)
 (3)
(3)
 、
、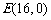 、
、 、
、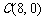
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值
索道在BC上方时,悬空高度
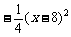


当 时,
时,
∴索道的最大悬空高度为 米.
米.
16、(2006湖南长沙)我市某乡 两村盛产柑桔,
两村盛产柑桔, 村有柑桔200吨,
村有柑桔200吨, 村有柑桔300吨.现将这些柑桔运到
村有柑桔300吨.现将这些柑桔运到 两个冷藏仓库,已知
两个冷藏仓库,已知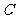 仓库可储存240吨,
仓库可储存240吨,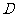 仓库可储存260吨;从
仓库可储存260吨;从 村运往
村运往 两处的费用分别为每吨20元和25元,从
两处的费用分别为每吨20元和25元,从 村运往
村运往 两处的费用分别为每吨15元和18元.设从
两处的费用分别为每吨15元和18元.设从 村运往
村运往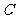 仓库的柑桔重量为
仓库的柑桔重量为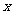 吨,
吨, 两村运往两仓库的柑桔运输费用分别为
两村运往两仓库的柑桔运输费用分别为 元和
元和 元.
元.
(1)请填写下表,并求出 与
与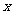 之间的函数关系式;
之间的函数关系式;
 |
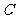 |
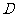 |
总计 |
 |
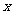 吨 吨 |
|
200吨 |
 |
|
|
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
(2)试讨论 两村中,哪个村的运费较少;
两村中,哪个村的运费较少;
(3)考虑到 村的经济承受能力,
村的经济承受能力, 村的柑桔运费不得超过4830元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值.
村的柑桔运费不得超过4830元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值.
解:
 |
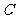 |
 |
总计 |
 |
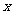 吨 吨 |
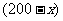 吨 吨 |
200吨 |
 |
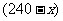 吨 吨 |
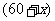 吨 吨 |
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
 ,
, .
.
(2)当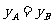 时,
时,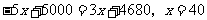 ;
;
当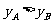 时,
时, ;
;
当 时,
时,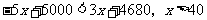 .
.
 当
当 时,
时,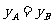 即两村运费相等;当
即两村运费相等;当 时,
时,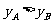 即
即 村运费较少;当
村运费较少;当 时,
时, 即
即 村费用较少.
村费用较少.
(3)由 得
得

设两村运费之和为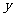 ,
, .
.
即: .
.
又 时,
时,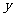 随
随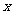 增大而减小,
增大而减小,
 当
当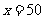 时,
时,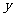 有最小值,
有最小值, (元).
(元).
答:当 村调往
村调往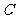 仓库的柑桔重量为50吨,调往
仓库的柑桔重量为50吨,调往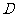 仓库为150吨,
仓库为150吨, 村调往
村调往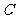 仓库为190吨,调往
仓库为190吨,调往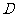 仓库110吨的时候,两村的运费之和最小,最小费用为9580元.
仓库110吨的时候,两村的运费之和最小,最小费用为9580元.
15、(2006贵州贵阳)某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个;
(1)假设销售单价提高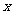 元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个;(用含
元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个;(用含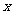 的代数式表示)
的代数式表示)
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?
解:(1)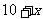 ,
,
(2)设月销售利润为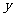 元
元
由题意得: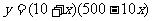
整理得: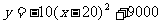
当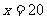 时,
时,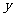 有最大值9000
有最大值9000

答:8000元不是最大利润,最大利润是9000元,此时篮球售价为70元;
14、(2006湖北宜昌)小资料:财政预计,三峡工程投资需2039亿元,由静态投资901亿元、贷款利息成本a亿元、物价上涨价差(a+360)亿元三部分组成.但事实上,因国家调整利率,使贷款利息减少了15.4%;因物价上涨幅度比预测要低,使物价上涨价差减少了18.7%.
2004年三峡电站发电量为392亿度,预计2006年的发电量为564.48亿度,这两年的发电量年平均增长率相同.若发电量按此幅度增长,到2008年全部机组投入发电时,当年的发电量刚好达到三峡电站设计的最高年发电量.从2009年起,拟将三峡电站和葛洲坝电站的发电收益全部用于返还三峡工程投资成本.葛洲坝年发电量为270亿度,国家规定电站出售电价为0.25元/度.
(1)因利息调整和物价上涨幅度因素使三峡工程总投资减少多少亿元?(结果精确到1亿元)
(2)请你通过计算预测:大约到哪一年可以收回三峡工程的投资成本?
解:⑴由题意可知:901+a+(a+360)=2039 .
解得:a=389.
三峡工程总投资减少得资金为:15.4%a+18.7%(a+360)
=0.154×389×0.187×(389+360)=199.969≈200(亿元)
⑵设2004年到2006年这两年的发电量平均增长率为x,,则依题意可知:
392(1+x)2=573 .
解得:x1≈21%,,x2≈-2.21%(应舍去)(无此结论不扣分)
2008年的发电量(即三峡电站的最高年发电量):
573(1+21%)2=839(亿度)
2009年起,三峡电站和葛洲坝电站的年发电总收益为:
(839+270)×0.25=277.25(亿元)
收回三峡电站工程的投资成本大约需要的年数: ≈6.6(年)
≈6.6(年)
∴到2015年可以收回三峡电站工程的投资成本.
注:学生因简单叙述或无文字叙述直接得出计算结果不扣分.
13、 (2006山东青岛)小明和小亮用如下的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方公平吗?请说明理由;若不公平,请你修改规则使游戏对双方公平.
(2006山东青岛)小明和小亮用如下的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方公平吗?请说明理由;若不公平,请你修改规则使游戏对双方公平.
解:
|
第二次 第一次 |
红 |
黄 |
蓝 |
|
红 |
(红,红) |
(红,黄) |
(红,蓝) |
|
黄 |
(黄,红) |
(黄,黄) |
(黄,蓝) |
|
蓝 |
(蓝,红) |
(蓝,黄) |
(蓝,蓝) |
从表中可以得到:P(小明获胜)= ,P(小亮获胜)=
,P(小亮获胜)= .
.
∴小明的得分为 ×1=
×1= , 小亮的得分为
, 小亮的得分为  ×1=
×1=  .
.
∵  >
> ,∴游戏不公平.
,∴游戏不公平.
修改规则不惟一.如若两次转出颜色相同或配成紫色,则小明得4分,否则小亮得5分.
12、(2006山东青岛)2006年青岛市春季房交会期间,某房地产公司对参加本次房交会的消费者进行了随机问卷,共发放1200份调查问卷,实际收回1000份.该房地产公司根据问卷情况,作了以下两方面的统计.
I.根据被调查消费者年收入情况制成的统计表:
|
年收入(元) |
2万以下 |
2万-4万 (不含4万) |
4万-6万 (不含6万) |
6万-8万 (不含8万) |
8万以上 |
|
各段被调查消费者人数占总被调查消费者人数的百分比 |
50% |
26% |
14% |
7% |
3% |
 II.根据被调查消费者打算购买不同住房面积的人数情况制成的扇形统计图:
II.根据被调查消费者打算购买不同住房面积的人数情况制成的扇形统计图:
根据上述信息,解决下列问题:
(1)被调查的消费者平均年收入为 万元.(提示:在计算时,2万元以下的都看成1万元,2万-4万元的都看成3万元,依此类推,8万元以上的都看成9万元)
(2)打算购买80 m2-100 m2 的消费者人数为 人.
(3)如果你是该房地产公司的开发商,请你从建房面积等方面谈谈你今后的工作打算(不超过30字).
解:(1)2.74.
(2)360.
(3)只要学生回答合理即可.
11、(2006山东济南)某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图1,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
 (1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积
(1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积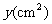 与
与 (见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有信息,在表中空白处填上适当的数、式,并完成
(见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有信息,在表中空白处填上适当的数、式,并完成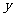 取最大值时的设计示意图;
取最大值时的设计示意图;
|
横截面图形 |
|
 |
 |
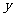 与 与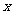 的函数关系式 的函数关系式 |
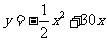 |
|
 |
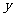 取最大值时 取最大值时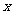 (cm)的值 (cm)的值 |
30 |
|
20 |
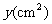 取得的最大值 取得的最大值 |
 450 450 |
|
 |
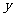 取最大值时的设计示意图 取最大值时的设计示意图 |
|
 |
 |
 (2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为
(2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为 的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
解:(1)表中空白处填写项目依次为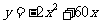 ;15;450.
;15;450.
表中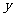 取最大值时的设计示意图分别为:
取最大值时的设计示意图分别为:

(2)小华的说法不正确.
因为腰长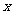 大于30cm时,符合题意的等腰梯形不存在,所以
大于30cm时,符合题意的等腰梯形不存在,所以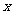 的取值范围不能超过30cm,因此研究性学习小组画出的图象是正确的.
的取值范围不能超过30cm,因此研究性学习小组画出的图象是正确的.
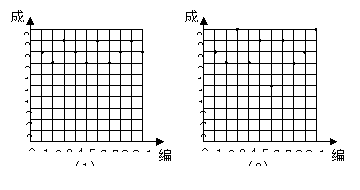
10、(2006山东济南)某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
|
班级 |
平均数(分) |
中位数(分) |
众数(分) |
|
(1)班 |
|
24 |
24 |
|
(2)班 |
24 |
|
|
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?
解:
(1)
|
班级 |
平均数(分) |
中位数(分) |
众数(分) |
|
(1)班 |
24 |
|
|
|
(2)班 |
|
24 |
21 |
(2) (名),
(名), (名).
(名).
答:(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀.
(3)(1)班的学生纠错的整体情况更好一些.
9、(2006山东济南)元旦联欢会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
纸环数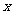 (个) (个) |
1 |
2 |
3 |
4 |
…… |
彩纸链长度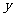 (cm) (cm) |
19 |
36 |
53 |
70 |
…… |
 (1)把上表中
(1)把上表中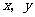 的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想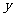 与
与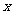 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
(2)教室天花板对角线长10m,现需沿天花板对角线各拉一
根彩纸链,则每根彩纸链至少要用多少个纸环?
解:(1)在所给的坐标系中准确描点.
由图象猜想到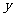 与
与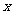 之间满足一次函数关系.
之间满足一次函数关系.
设经过 ,
, 两点的直线为
两点的直线为 ,则可得
,则可得
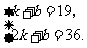 解得
解得 ,
, .即
.即 .
.
当 时,
时, ;当
;当 时,
时,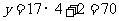 .
.
即点 都在一次函数
都在一次函数 的图象上.
的图象上.
所以彩纸链的长度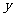 (cm)与纸环数
(cm)与纸环数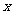 (个)之间满足一次函数关系
(个)之间满足一次函数关系 .
.
(2) ,根据题意,得
,根据题意,得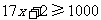 .
.
解得 .
.
答:每根彩纸链至少要用59个纸环.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com