
2.如果a、b、c为互不相等的实数,且满足关系式:b2+c2=2a2+16a+14
与bc=a2-4a-5,那么a的取值范围是________.
1. 如图1, 矩形内有两个相邻的正方形,面积分别为4和2,那么阴
影部分的面积为_________.
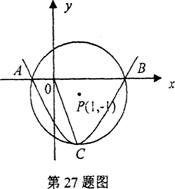
27.如图,在平面直角坐标系中,以点P(1,-1)为圆心,2为半径作圆,交x轴A、B两点,抛物线
y=ax2+bx+c(a>O)过点A、B,且顶点C在⊙P上.
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
[解析](1)作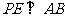 于
于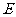 ,连接PA,则PA=2,PE=1, ∴
,连接PA,则PA=2,PE=1, ∴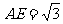
∵E点坐标为(1,0),∴A点坐标为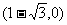 ,B点坐标为
,B点坐标为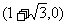
∴可设抛物线的解析式为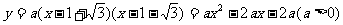
∴其顶点C的坐标为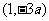
而⊙P的圆心P的坐标为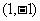 ,半径为2
,半径为2
∴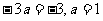
∴此抛物线的解析式为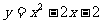
(2)设存在这样的点D,坐标为( )
)
∵线段OC与PD互相平分,∴四边形OPCD为平行四边形.
∵OD∥PC,P、C两点的横坐标相等,∴O、D两点的横坐标也相等.
∴D点坐标为(0,-2)
∴直线DC的解析式为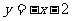 ,直线OP的解析式为
,直线OP的解析式为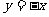
∴OP∥DC
∴抛物线上存在一点D(0,-2),使线段OC与PD互相平分.
[点评]本题较难.(1)类似于25题,(2)是存在性问题,这种题一般都假设要求的点存在,然后进行数学推导.要求对平行四边形的判定、一次函数、直线平行等知识熟练掌握.
26.如图,在⊙O中,弦AB⊥AC,AB=a,AC=b,弦AD平分∠BAC.求AD的长(用a、b表示).
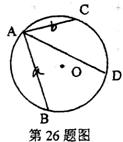
[解析]连接BC,BD,CD,设BC交AD于E
∵AB⊥AC, ∴BC经过O点.
∵AD平分∠BAC,∴
∴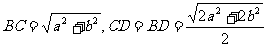
∵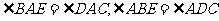 ,∴△ABE∽△ADC, ∴
,∴△ABE∽△ADC, ∴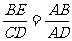
同理,△CDE∽△ADC, ∴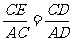
∴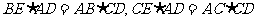 ,两式相加,得
,两式相加,得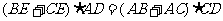
解得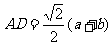
[点评]难题.方法较多,如应用正弦定理或者余弦定理等.解析中的方法充分利用了圆的性质,结合相似形求解.
25.矩形ABCD的边长AB=3,AD=2,将此矩形放在平面直角坐标系中,使AB在x轴的正半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线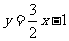 经过这两个顶点中的一个.
经过这两个顶点中的一个.
(1)求A、B、C、D四点坐标.
(2)以AB为直径作⊙M,记过A、B两点的抛物线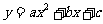 的顶点为P.
的顶点为P.
①若P点在⊙M和矩形内,求a的取值范围.
②过点C作CF切⊙M于E,交AD于F,当PF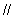 AB时,求抛物线的函数解析式.
AB时,求抛物线的函数解析式.
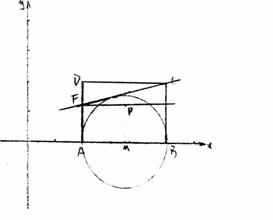
[解析](1)首先画图.设点A坐标为(x,0) 又∵AB=3 AD=2 且点A在点B 的左侧.AB在x轴的正半轴上.
又∵ABCD为矩形,则点B、C、D的坐标分别为(x+3,0),(x+3,2),(x,2)
∴直线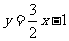 经过这两个顶点中的一个.当其经过点C时,
经过这两个顶点中的一个.当其经过点C时,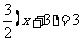 ∴x=-1
∴x=-1
又∵点A在x轴正半轴上 ∴x>0 ∴x=-1舍去
当其经过点D时,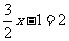 ∴x=2,符合题意.
∴x=2,符合题意.
∴A.B.C.D四点坐标分别为(2,0) (5,0) (5,2) (2,2)
(2)①∵此抛物线过点A.B
∴可设抛物线的解析式为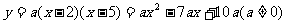
∴其顶点P的坐标为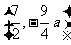
而⊙M的圆心M的坐标为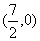 ,半径为
,半径为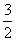
∴若P点在⊙M和矩形内,则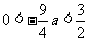 ,
,
∴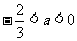 .
.
②设点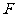 坐标为
坐标为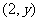 ,则
,则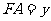
∵CF切⊙M于E,CB、FA均为⊙M的切线,故△CBM≌△CEM(HL),△FAM≌△FEM(HL)
∴CB=CE=2,FA=FE=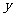 ,
,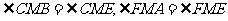
∴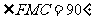
在Rt△FAM中,有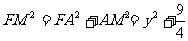
在Rt△CEM中,有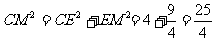
在Rt△CFM中,有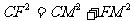
∴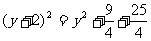
解得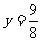
故P点纵坐标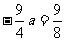 ,
,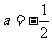
∴此抛物线的函数解析式为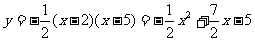
[点评]本题综合性较强,有相当难度.
(1)首先要能根据题意,正确的画出图形,写出四个点的坐标,还要注意分类讨论.求得解后要检验.
(2)①设抛物线解析式的时候,此题应根据题意设两点式.很多同学不动脑筋,只知道设一般式,然后用待定系数法,在这题里是比较繁琐的.得到P点坐标的表达式后,应注意到P点的横坐标是定值,等于M点的横坐标,如果不注意到这一点,也可能找不到最简捷的解法.
②题目条件众多且较复杂,要想考试时很快切入解题要点,需要在平时多练习、多思考.这题的关键是利用直线CF,FA,CB和圆的相切关系,判断并且证明两对全等三角形,然后利用勾股定理列方程求解.这是解决几何计算问题的常用手段.
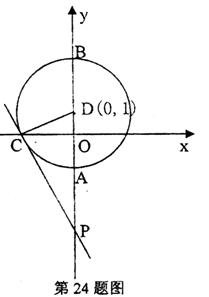
24.(本小题6分).己知:如图,⊙D交y轴于A、B,交x轴于C,过点C的直线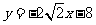 与y轴交于P,D点坐标(0,1)
与y轴交于P,D点坐标(0,1)
求证:PC是⊙D的切线.
[解析]∵直线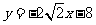 交于x轴于点C,交y轴于P
交于x轴于点C,交y轴于P
∴点C.P坐标分别为(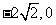 ),(0,-8)
),(0,-8)
∴OC=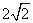 OP=8
OP=8
又∵∠COP=900
∴PC2=OC2+OP2
∴PC= 又∵
又∵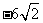 <0 ∴舍去
<0 ∴舍去
∵点D坐标为(0,1) ∴DO=1
又∵OC=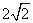 ∠DOC=900
∠DOC=900
∴DC2=DO2+OC2=9
∴DC=3或-3 又∵-3<0 ∴舍去
又∵DO=1 OP=8 ∴DP=9
又∵DP2=81=72+9=PC2+DC2
∴∠DCP=900即PC是⊙D的切线.
[点评]本题是一道综合题,考查的知识点比较多:坐标系、圆、一次函数、直线与圆的位置关系、坐标与长度之间的关系、勾股定理等,这种几何与代数结合的题,首先要求大家基本功扎实,其次还要能将所学的知识融会贯通,综合应用.
23.(本小题6分)如图.正方形ABCD中,E、F分别在边BC、CD上,∠EAF=450,BE=2,CF=3.
求:正方形的边长.
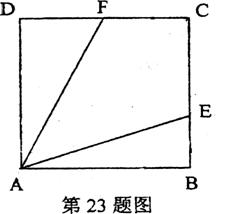
[解析]法一:延长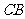 至
至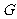 ,连接
,连接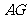 、
、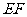 ,先证明△
,先证明△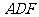 ≌△
≌△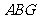 (SAS),
(SAS),
故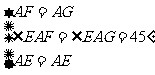
有△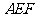 ≌△
≌△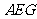
所以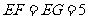
故由勾股定理,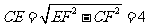
从而正方形的边长为4+2=6.
法二:连结AC,作FG垂直于AC于G
∴∠CAB=450即∠CAE+∠EAB=450,∠DCA=450
又∵∠FAG+∠EAC=450
∴∠FAG=∠EAB
又∵四边形ABCD为正方形
∴∠EBA=900=∠FGA
∴△EAB∽△FAG
又∵∠FGC=900 ∠FCG=450
∴△FGC为等腰直角三角形
又∵FC=3 ∴FG2+GC2=9
∴FG=GC=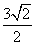
又∵△EAB∽△FAG
∴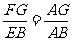
∴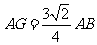
又∵∠CAB=450 ∠B=900 ∴AB=BC 且AB2+BC2=AC2
∴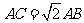
∴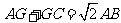
∴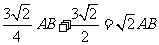
∴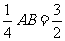
∴AB=6 即正方形的边长为6.
[点评]本题是一类非常非常常见的题型,.方法一的辅助线的画法,实质上是利用旋转,将分散的条件集中起来,通过三角形全等、勾股定理来解决问题.方法二是某学生在实际考试中的做法,是利用相似形、三角形全等、等腰直角三角形、方程等方法解决问题,反映出这名学生扎实的功底,但有点繁琐了.像这样的常见题型和基本图形要熟悉.
21. (本小题7分).机械加工需用油进行润滑以减小摩擦,某企业加工一台大型机械设备润滑用油量为90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克.为了建设节约型社会,减少油耗,该企业的甲乙两个车间都组织了人员为减少实际油耗量进行攻关.
(1)甲车间通过技术革新后,加工一台大型机械设备润滑用油量下降到70千克,用油的重复利用率仍为60%,问甲车间技术革新后,加工一台大型机械设备的实际耗油量是多少千克?
(2)乙车间通过技术革新后,不仅降低了润滑用油量,同时也提高了重复利用率,并且发现在技术革新前的基础上,润滑用油量每减少1千克,用油的重复利用率将增加1.6%,这样乙车间加工一台大型机械设备的实际耗油量下降到12千克。问乙车间技术革新后,加工一台大型机械设备的润滑用油量是多少千克?用油的重复利用率是多少?
[解析](1)∵加工一台大型机械设备润滑用油量下降到70千克.
又∵用油的重复利用率仍为60%,即实际耗油率为100%-60%=40%
∴实际耗油量=70×40%=28(千克)
答:技术革新后,加工一台大型机械设备的实际耗油量是28千克.
(2)解:设润滑用油量减少了x千克,所以用油的重复利用率增加了0.016x.
根据题意:得
(90-x)(1-0.6-0.016x)=12
(90-x)(0.4-0.016x)=12
(90-x)(400-16x)=1200
解得:x1=15 x2=100
又∵x2=100>90 ∴舍去
∴加工一台大型机械设备的润滑用油量为90-15=75(千克)
用油的重复利用率为60%+15×1.6%=84%
答:加工一台大型机械设备的润滑用油量是75千克.用油的重复利用率是84%.
[点评]应用题最重要的是读懂题意.比如本题中出现的“用油的重复利用率”,到底什么意思?一来可以照字面理解,二来题目中有解释:“按此计算,加工一台大型机械设备的实际耗油量为36千克”.总之,如果题目意思没有弄明白,这样的题是没法完成的.本题还考了列一元二次方程解应用题.方程的解要符合实际题目的要求.
20. (本小题6分).小明、小亮和小强三人准备下象棋,他们约定用 “抛硬币”的游戏方式来确定哪两个人先下棋,规则如下图:

(1)请你画出表示游戏一个回合所有可能出现的结果的树状图:
(2)求一个回合能确定两人先下棋的概率.
[解析]
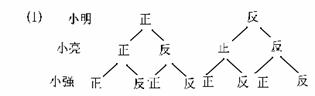
(2)根据树状图可得,所有可能出现的情况为8种,能一个回合确定两人先下棋的可能为6种.
∴一个回合能确定两人先下棋的概率为
6÷8=0.75
答:一个回合能确定两人先下棋的概率为0.75.
[点评]本题首先要将题读懂,明白游戏的规则,然后细心画出树状图就可以基本上解决问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com