
5、已知一元二次方程的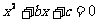 的两个根是1和3,则
的两个根是1和3,则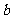 ,
,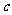 的值分别是
的值分别是
(A) 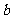 = 4,
= 4, 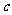 =-3
(B)
=-3
(B) 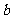 =3,
=3, 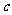 =2
=2
(C) 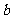 =-4,
=-4, 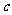 =3
(D)
=3
(D) 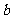 = 4,
= 4, 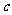 =3
=3
4、用配方法解方程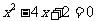 ,下列配方的结果正确的是
,下列配方的结果正确的是
(A)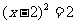 (B)
(B)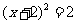 (C)
(C)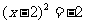 (D)
(x-2)2=0
(D)
(x-2)2=0
3、把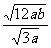 化简后得
化简后得
(A)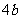 (B)
(B) 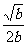 (C)
(C)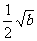 (D)
(D) 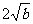
2、如果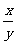 =
= 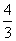 ,那么
,那么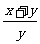 的值是
的值是
(A) 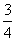 (B)
(B)
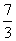 (C)
(C)
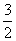 (D)
(D)
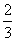
1、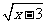 实数范围内有意义,则x的取值范围是
实数范围内有意义,则x的取值范围是
(A) x>3 (B) x<3 (C) x≥3 (D) x≤3
26.(12分)如图,对称轴为直线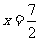 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(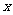 ,
,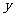 )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与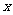 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量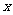 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
 ②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
25. (本题满分12分)
某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系。
|
x(元/件) |
35 |
40 |
45 |
50 |
55 |
|
y (件) |
550 |
500 |
450 |
400 |
350 |
(1) 试求y与x之间的函数表达式;
(2) 设公司试销该产品每天获得的毛利润为s(元),求s与x之间的函数表达式(毛利润=销售总价-成本总价);
(3) 当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?最大利润是多少?此时每天的销售量是多少?
24.(8分)文物探测队探测出某建筑物下面有地下文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距20米的A、B两处,用仪器测文物C,探测线与地面的夹角分别是30°和60°,求该文物所在位置的深度
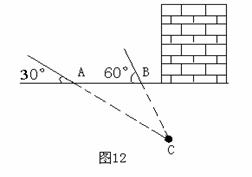 (精确到0.1米).
(精确到0.1米).
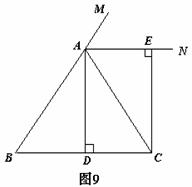
23、(本题满分8分)
已知:如图9,在ΔABC中,AB=AC,AD⊥BC,垂足为点D,AN是ΔABC外角∠CAM的平分线,
CE⊥AN,垂足为点E。
(1)求证:四边形ADCE为矩形;
(2)当ΔABC满足什么条件时,四边形ADCE是一个正方形?
并给出证明。
22.(8分)一天小伟帮助妈妈做家务,负责清洗三个只有颜色不同的有盖茶杯,洗完后突然停电了,小伟只好把茶杯和杯盖随机地搭配在一起,求全部搭配正确的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com