2．课前热身

　　 互动1

　　 师：请同学们思考一下，他这样测行吗？有什么依据吗？

　　 生：他这样测可以．因为由三角形的一个外角等于两个不相邻的两个内角和可以求出∠B=30°，又因为∠B=∠C，所以AB=AC．

　　 师：很好．军军这种方法其实就是利用“等角对等边”，那么同学们是怎样知识等腰三角形的这个识别方法的呢？

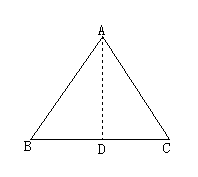生：用折纸的方法．如图所示，△ABC中，∠B=∠C，利用刻度尺找到BC的中点D，连结AD，然后沿AD对折，观察发现AB、AC完全重合，于是得到AB=AC．

　　 明确　 回顾在第9章得出的“等角对等边”这个识别等腰三角形的重要方法．

1．情境导入

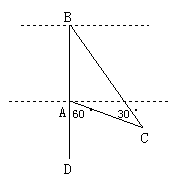
军军想利用学过的知识测一测河宽(如图所示)．他先沿着垂直于河岸的方向在河两岸分别选定两点A、B，再从A点到C点，测得∠C=30°，∠DAC=60°，量一量AC的长度就是河宽．

2．经历探索证明方法的过程，逐步培养学生逻辑推理的能力．

1．掌握等腰三角形的判定定理、性质定理以及斜边、直角边定理的证明．

　　 (1)链接生活

　　 通过这节课的学习，请你设计一种方案，测出操场上旗杆的高度．

　　 (2)巩固练习

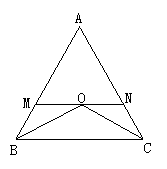
①如图所示，在△ABC中，∠ABC=∠ACB，∠ABC与∠ACB的平分线交于点O，过O作MN∥BC交AB于M，交AC于N，则图中共有 　5　 个等腰三角形．

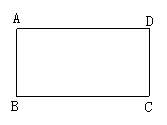
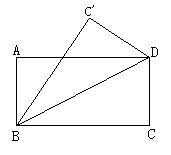
②将一张矩形纸片ABCD沿对角线对折(如图所示)，求证：重叠部分是一个等腰三角形．(提示：利用矩形对边平行的性质及折叠过程中的全等三角形证明)

　　 (四)板书设计

5．学习小结

　　 (1)引导学生作知识总结，通过本节课的学习掌握了等腰三角形的判定定理、性质定理的证明，同时还得出“三线合一”这一重要性质，并且利用等腰三角形性质定理证明了“H．L”定理．

　　 (2)教师扩展：今天学习的几条定理是今后证明两条线段相等、两个角相等及两条直线互相垂直的重要依据．

4．达标反馈

　　 (1)填空

　　 ①根据等腰三角形三线合一的性质，在△ABC中，

　　 (a)∵AB=AC，AD⊥BC，∴∠BAD=∠CAD，BD=CD．

　　 (b)∵AB=AC，AD是中线，∴∠BAD=∠CAD，AD⊥BC．

　　 (c)∵AB=AC，AD是角平分线，∴AD⊥BC，BD=CD．

　　 ②等边三角形各角都 　相等 　，且每一个角都等于　 60° 　．

　　 ③等腰直角三角形的每个锐角为　 45° 　，斜边上的高把直角分成的两个锐角为　 45° 　．

　　 ④三角形中，若有两个角的平分线都垂直于对边，则此三角形是　 等边 　三角形．

　　 (2)证明：

　　 ①等腰三角形顶角的外角平分线与底边平行．

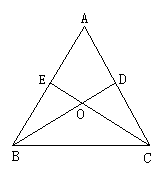
　　 ②如图所示，△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE交于O点．

　　 求证：1°△BCD≌△CBE；2°△BOE≌△COD．

　　 [答案]　 (略)

2．课前热身

　　 互动1

　　 师：请同学们思考一下，他这样测行吗？有什么依据吗？

　　 生：他这样测可以．因为由三角形的一个外角等于两个不相邻的两个内角和可以求出∠B=30°，又因为∠B=∠C，所以AB=AC．

　　 师：很好．军军这种方法其实就是利用“等角对等边”，那么同学们是怎样知识等腰三角形的这个识别方法的呢？

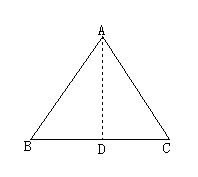生：用折纸的方法．如图所示，△ABC中，∠B=∠C，利用刻度尺找到BC的中点D，连结AD，然后沿AD对折，观察发现AB、AC完全重合，于是得到AB=AC．

　　 明确　 回顾在第9章得出的“等角对等边”这个识别等腰三角形的重要方法．

1．情境导入

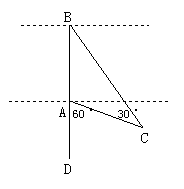
军军想利用学过的知识测一测河宽(如图所示)．他先沿着垂直于河岸的方向在河两岸分别选定两点A、B，再从A点到C点，测得∠C=30°，∠DAC=60°，量一量AC的长度就是河宽．