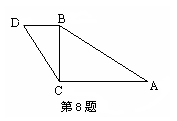
8.如图，已知∠ACB=∠CBD=90^o，BC=a，AC=b，当CD=(　　 )时，△CDB∽△ABC.

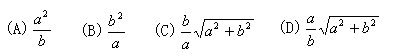
　　 (A)锐角三角形　　 (B)直角三角形　　

(C)钝角三角形　　 (D)不能确定形状

7.甲、乙、丙三人放风筝，各人放出的风筝线长分别为60m、50m、40m，线与地平面所成的角分别为30^o、45^o、60^o，假设风筝线近似看作是拉直的，则所放风筝最高的是(　　 ).

　　 (A)甲　　　 (B)乙　　 (C)丙　　 (D)不能确定

5.已知等腰梯形的上、下底边的长分别为6cm和16cm，腰长13cm，则它的面积是　　　　　 .

4.在坡度为1:3.5的山坡上上行500米，则垂直高度上升了　　　　 米.在这样的山坡上植树，要求株距(相邻两树间的水平距离)是3米，则斜坡上相邻两树间的坡面距离应是　　　　　 米 (精确到0.1米).

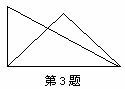
3.一副三角板放成如图所示的位置，如果重合的一条边长48厘米，则其余几条边的长度分别为　　　　　　　　　　　　　 .

2. △ABC中∠A=40^o，∠C=90，a=4.2，则b≈　　　　　 ，c≈　　　　　 (保留2个有效数字).

1.已知直角三角形中两条边的长分别是6cm和8cm，则第三条边长为　　　　　 .

27、(12分) 某公司现有甲、乙两种品牌的计算器，甲品牌计算器有A、B、C三种不同的型号，乙品牌计算器有D、E两种不同的型号，某中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器．

(1)写出所有的选购方案(利用树状图或列表方法表示)；

(2)如果(1)中各种选购方案被选中的可能性相同，那么A型号计算器被选中的概率是多少？

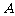(3)现知该中学购买甲、乙两种品牌计算器共40个(价格如图所示)，恰好用了1000元人民币，其中甲品牌计算器为型号计算器，求购买的型号计算器有多少个？

26、小颖和小红两位同学在学习“概率”时，做投掷骰子(质地均匀的正方体)实验，他们共做了60次实验，实验的结果如下：

(1)计算“3点朝上”的频率和“5点朝上”的频率．(4分)

(2)小颖说：“根据实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次．”小颖和小红的说法正确吗？为什么？(4分)

(3)小颖和小红各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．(4分)

25、杨华与季红用5张同样规格的硬纸片做拼图游戏，正面如图1所示，背面完全、一样。将他们背面朝上搅匀后，同时抽出两张，规则如下：

　　 当两张硬纸片上的图形可拼成电灯或小人时，杨华得1分；当两张硬纸片上的图形可拼成房子或小山时，季红得1分 (如图2所示)

　　 问题：游戏规则对双方公平吗? 说明理由；若你认为不公平，如何修改游戏规则才能使游戏对双方公平? (10分)

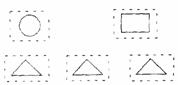
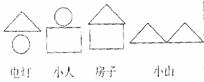
图1　　　　　 　　　　　　　　　　图2