2．提供学生自主探索和合作交流的平台，让学生参与探寻解题思路和方法的过程，适当选编相关例题给学生分析、思考、讨论．以下例题供参用：

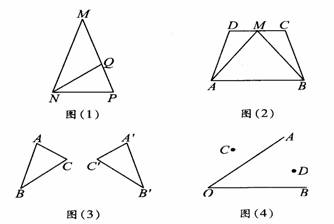
　　 (1)如图(1)，在△MNP中，MN=MP，点Q在MP上，且NP=NQ=MQ，①找出图中相等的角，并说明理由；②求∠M的度数．

　　 (2)如图(2)，在等腰梯形ABCD中，M是上底CD的中点，连接AM、BM，△AMB是等腰三角形吗?为什么?(试用两种方法说理)

　　 (3)图(3)中的△ABC和△A’B’C’成轴对称，试用不同的方法作出对称轴．

(4)在图(4)中找一点P，使点P到∠AOB两边的距离相等，且到C、D两点的距离也相等，试用直尺、圆规作图，并保留作图痕迹．

1．让学生用自己的语言总结归纳本章所学的知识，引导学生从以下几方面进行回忆与反思：

　　 (1)轴对称与轴对称图形的特征、区别与联系；

　　 (2)比较线段、角、等腰三角形、等边三角形、等腰梯形的对称性；

　　 (3)线段的垂直平分线和角平分线，等腰三角形和等腰梯形的性质类比；

　　 (4)如何作简单图形经过两次轴对称后的图形．

　　 在组织学生进行回忆和反思的活动中，教师要关注学生自己对已学的数学知识的理解程度，尊重学生在反思交流中所表现出的不同水平，鼓励他们发表自己的见解，帮助他们系统地建构知识网络．

3．在解决问题和与他人合作交流的过程中，不断发展合情推理，进一步学习有条理地思考和表达，真切地感受“言之有理，落笔有据”的必要性．

[教学过程设计建议]

2．进一步巩固和掌握轴对称性质和简单的轴对称图形--线段、角、等腰三角形、等边三角形、等腰梯形的性质，并能运用这些性质解决问题。

1．回顾和整理本章所学知识，用自己喜欢的方式进行总结和归纳，构建本章知识结构框架，使所学知识系统化．

25、　 在△ABC中，AB=AC，AB的垂直平分线交AB于N，交BC的延长线于N，∠A=40°。

(1)求∠M的度数。

(2)若将∠A的度数改为80°，其余条件不变，再求∠M的大小。

(3)你发现怎样的规律？并说明理由。

(4)将(1)中的∠A改为钝角，(3)中的规律仍成立吗？若不成立，应加以怎样修改。

24、已知D是等腰三角形ABC底边BC上的一点，它到两腰AB,AC的距离DE，DF，如图，当D在什么位置时，DE=DF？并说明理由。

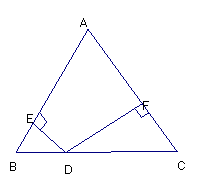
(第24题)　　　　　　

23、如图，D是等边△ABC内一点，DB=DA，BP=BA，∠DBP=∠DBC，求∠P的度数。

(第23题)

22、等腰梯形ABCD中，AD∥BC，E是AD延长线上的一点，CE=CD。∠B与∠E相等吗？为什么？

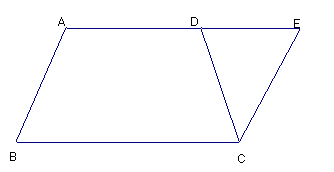
　　　　　　　　　　　　　　　　　　　　　 (第22题)

21、如图，在△ABC中，∠B=2∠C，BD平分∠B，DE⊥AB(E在AB之间)DF⊥BC于F。已知BD=5，DE=3，BF=4，试求△DFC的周长。

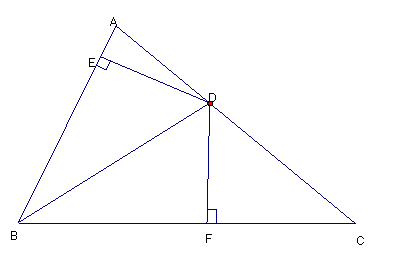
　　　　　　　　　　　　　　　　　　　　　　　　 (第21题)