
(三)应用、探究
1、如图1-2,用两根长度均为l cm的绳子,分别围成一个正方形和圆
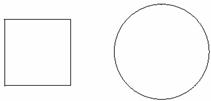 图1-2
图1-2
(1)如果要使正方形的面积不大于25 cm2, 那么绳长l应满足怎样的关系式?
(2)如果要使圆的面积不小于100 cm2,那么绳长l应满足怎样的关系式?
(3)当l=8时,正方形和圆的面积哪个大?l=12呢?
(4)你能得到什么猜想?改变l的取值,再试一试.
(二)思索、交流
①a,b两个实数在数轴上的对应点如图1-1所示:

图1-1
用“<”或“>”号填空:
(1)a__________b;(2)|a|__________|b|;
(3)a+b__________0;(4)a-b__________0;
(5)a+b__________a-b;(6)ab__________a.
②用不等式表示:
(1)x的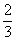 与5的差小于1;_____________________________________
与5的差小于1;_____________________________________
(2)x与6的和大于9;__________________________________________
(3)8与y的2倍的和是正数;___________________________________
(4)a的3倍与7的差是负数;___________________________________
(5)x的4倍大于x的3倍与7的差;______________________________
(6)x的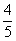 与1的和小于-2;____________________________________
与1的和小于-2;____________________________________
(7)x与8的差的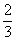 不大于0. _____________________________________
不大于0. _____________________________________
③当x=2时,不等式x+3>4成立吗?
当x=1.5时,成立吗?
当x=-1呢?
(一)自学、相信自己
①举出现实生活中的不等关系;______________________________________________________________________________________________________________________________________
②用不等式表示
(1)a是正数;____________________________________________
(2)a是负数;____________________________________________
(3)a与6的和小于5;_____________________________________
(4)x与2的差小于-1;____________________________________
(5)x的4倍大于7;_______________________________________
(6)y的一半小于3. ________________________________________
1、自学课本121页到123页,写下疑惑摘要:
_________________________________________________________________________________________________________________________________________________________________________________________________________
[例10]在欧洲足球锦标赛中,共有16支队伍参加比赛,争夺象征欧洲足球最高荣誉的“德劳内杯”.16支队伍被分成4个小组,进行单循环赛(即每个队需同其他三个队各赛一场),胜一场积3分,平一场积1分,负一场积0分,每组按照积分的前两名出线进入前八强,每个队在小组赛中需积多少分,才能确保出线? [思考与分析]根据题意,只有小组赛中的积分的前两名才能出线,我们可以分几种情况来讨论出线积分的多少. (1)若某一队三战全胜积9分,则同组的另一小队需保证小组第二才有出线的希望,在剩下的两场比赛中,它有六种可能:两场全胜积6分,一胜一平积4分,一胜一负积3分,两平积2分,一平一负积1分,两负积0分.(三场比赛,肯定有一场负)因此,在这种情况中,至少积6分才能确保出线; (2)若某一队三战两胜一平积7分,则小组第二至少要两胜积6分才能出线; (3)若某一队三战两胜一负积6分,则其他两个队也可能三战两胜一负积6分,这样三队同积6分,不能确保小组出线. 由以上思考讨论可知,在小组赛中,积分可能出现三个队积分相同,为了确保出线,至少需积7分,才能保证以小组第二的身份出线. 解:需7分. [小结]通过解题过程我们知道做这类题的时候要注意:在足球比赛中,一般按积分多少排名次;积分相等的两队,净胜球数多的队名次在前;积分、净胜球数都相等的球队,进球数多的队名次在前;分析有关足球比赛的问题时,不能单纯的利用不等关系判断,还要注意到相互之间的胜负关系.
第五节、竞赛数学
[例1]满足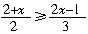 的x的值中,绝对值不超过11的那些整数之和等于
.
[思考与分析] 要求出那些整数之和,必须求出不等式的绝对值不超过11的整数解,因此我们应该先解不等式.
解: 原不等式去分母,得
3(2+x)≥2(2x-1),
去括号,移项,合并同类项,得
-x≥-8,即x≤8.
满足x≤8且绝对值不超过11的整数有0,±1,±2,±3,±4,±5,±6,±7,±8,-9,-10,-11.
这些整数的和为(-9)+(-10)+(-11)=-30.
[例2] 如果关于x的一元一次方程3(x+4)=2a+5的解大于关于x的方程
的x的值中,绝对值不超过11的那些整数之和等于
.
[思考与分析] 要求出那些整数之和,必须求出不等式的绝对值不超过11的整数解,因此我们应该先解不等式.
解: 原不等式去分母,得
3(2+x)≥2(2x-1),
去括号,移项,合并同类项,得
-x≥-8,即x≤8.
满足x≤8且绝对值不超过11的整数有0,±1,±2,±3,±4,±5,±6,±7,±8,-9,-10,-11.
这些整数的和为(-9)+(-10)+(-11)=-30.
[例2] 如果关于x的一元一次方程3(x+4)=2a+5的解大于关于x的方程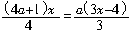 的解,那么(
).
的解,那么(
).
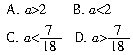 [思考与分析] 这道题把方程问题转化为解不等式问题,利用了转化的数学思想.由于第一个方程的解大于第二个方程的解,只要先分别解出关于x的两个方程的解(两个解都是关于a的式子),再令第一个方程的解大于第二个方程的解,就可以求出问题的答案.
解: 关于x的方程3(x+4)=2a+5的解为
[思考与分析] 这道题把方程问题转化为解不等式问题,利用了转化的数学思想.由于第一个方程的解大于第二个方程的解,只要先分别解出关于x的两个方程的解(两个解都是关于a的式子),再令第一个方程的解大于第二个方程的解,就可以求出问题的答案.
解: 关于x的方程3(x+4)=2a+5的解为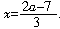 关于x的方程
关于x的方程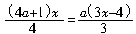 的解为
的解为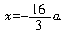 由题意得
由题意得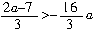 ,解得
,解得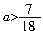 .因此选D.
[例3] 如果
.因此选D.
[例3] 如果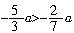 ,2+c>2,那么( ).
A. a-c>a+c B.
c-a>c+a
C. ac>-ac
D. 3a>2a
[思考与分析] 已知两个不等式分别是关于a和c的不等式,求得它们的解集后,便可以找到正确的答案.
解: 由
,2+c>2,那么( ).
A. a-c>a+c B.
c-a>c+a
C. ac>-ac
D. 3a>2a
[思考与分析] 已知两个不等式分别是关于a和c的不等式,求得它们的解集后,便可以找到正确的答案.
解: 由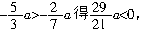 所以a<0.
由2+c>2,得c>0,则有-c<c.
两边都加上a,得a-c<a+c,排除A;
由a<0,c>0,得ac<0,-ac>0,从而ac<-ac,排除C;
由a<0,两边都加上2a,得3a<2a,排除D.
答案应该选B,事实上,由a<0,得-a>0,从而-a>a,两边同时加上c,可得c-a>c+a.
[例4] 四个连续整数的和为S,S满足不等式
所以a<0.
由2+c>2,得c>0,则有-c<c.
两边都加上a,得a-c<a+c,排除A;
由a<0,c>0,得ac<0,-ac>0,从而ac<-ac,排除C;
由a<0,两边都加上2a,得3a<2a,排除D.
答案应该选B,事实上,由a<0,得-a>0,从而-a>a,两边同时加上c,可得c-a>c+a.
[例4] 四个连续整数的和为S,S满足不等式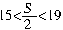 ,这四个数中最大数与最小数的平方差等于 .
[思考与分析] 由于四个数是连续整数,我们欲求最大值与最小值,故只须知四数之一就行了,由它们的和满足的不等式就可以求出.
解: 设四个连续整数为m-1,m,m+1,m+2,它们的和为S=4m+2.
由
,这四个数中最大数与最小数的平方差等于 .
[思考与分析] 由于四个数是连续整数,我们欲求最大值与最小值,故只须知四数之一就行了,由它们的和满足的不等式就可以求出.
解: 设四个连续整数为m-1,m,m+1,m+2,它们的和为S=4m+2.
由 <19,
解得7<m<9.
由于m为整数,所以m=8,则四个连续整数为7,8,9,10,因此最大数与最小数的平方的差为102-72=51.
<19,
解得7<m<9.
由于m为整数,所以m=8,则四个连续整数为7,8,9,10,因此最大数与最小数的平方的差为102-72=51.
从数轴上看,一个数的绝对值就是表示这个数的点离开原点的距离.但除零以外,绝对值都是表示两个数的绝对值,即一个数与它相反数的绝对值是一样的.由于这个性质,含有绝对值号的不等式的求解过程出现了一些新特点.
一个实数a的绝对值记作∣a∣,指的是由a所惟一确定的非负实数:
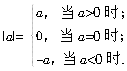 含绝对值的不等式的性质:
(1) ∣a∣≥∣b∣
含绝对值的不等式的性质:
(1) ∣a∣≥∣b∣ b≤|a|或b≥-|a|,
∣a∣≤∣b∣
b≤|a|或b≥-|a|,
∣a∣≤∣b∣ ∣b∣≤a≤∣b∣;
(2) ∣a∣-∣b∣≤∣a+b∣≤∣∣a∣+∣b∣;
(3) ∣a∣-∣b∣≤∣a-b∣≤∣a∣+∣b∣.
由于绝对值的定义,含有绝对值号的代数式无法进行统一的代数运算.通常的手法是按照绝对值符号内的代数式取值的正、负情况,去掉绝对值符号,转化为不含绝对值号的代数式进行运算,即含有绝对值号的不等式的求解,常用分类讨论法.在进行分类讨论时,要注意所划分的类别之间应该不重、不漏.下面结合例题予以分析.
[例5]解不等式 |x-5|-|2x+3|<1.
[分析] 关键是去掉绝对值符号前后的变号.分三个区间讨论:
∣b∣≤a≤∣b∣;
(2) ∣a∣-∣b∣≤∣a+b∣≤∣∣a∣+∣b∣;
(3) ∣a∣-∣b∣≤∣a-b∣≤∣a∣+∣b∣.
由于绝对值的定义,含有绝对值号的代数式无法进行统一的代数运算.通常的手法是按照绝对值符号内的代数式取值的正、负情况,去掉绝对值符号,转化为不含绝对值号的代数式进行运算,即含有绝对值号的不等式的求解,常用分类讨论法.在进行分类讨论时,要注意所划分的类别之间应该不重、不漏.下面结合例题予以分析.
[例5]解不等式 |x-5|-|2x+3|<1.
[分析] 关键是去掉绝对值符号前后的变号.分三个区间讨论: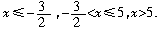 解: (1)当当x≤
解: (1)当当x≤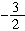 时,原不等式化为-(x-5)-[-(2x+3)]<1,
解得x<-7,结合x≤
时,原不等式化为-(x-5)-[-(2x+3)]<1,
解得x<-7,结合x≤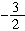 ,故x<-7是原不等式的解;
(2)当
,故x<-7是原不等式的解;
(2)当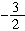 <x≤5时,原不等式化为
-(x-5)-(2x+3)<1,
解得
<x≤5时,原不等式化为
-(x-5)-(2x+3)<1,
解得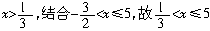 是原不等式的解;
(3)当x>5时,原不等式化为:
x-5-(2x+3)<1,
解得x>-9,结合x>5,故x>5是原不等式的解.
综合(1),(2),(3)可知,
是原不等式的解;
(3)当x>5时,原不等式化为:
x-5-(2x+3)<1,
解得x>-9,结合x>5,故x>5是原不等式的解.
综合(1),(2),(3)可知, 是原不等式的解.
是原不等式的解.
第六节、本章训练
基础训练题
1.不等式x+3<6的非负整数解为( ).
A. 1,2
B. 1,2,3
C. 1,2,0 D. 1,2,3,0
2.已知三个连续奇数的和不超过27且大于10,这样的数组共有( ).
A. 1个 B. 2个
C. 3个 D. 4个
3. 的值不小于-2,则a的取值范围是( ).
的值不小于-2,则a的取值范围是( ).
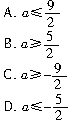 4.若
4.若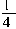 +2x的值不大于8-
+2x的值不大于8-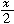 的值,那么x的正整数解是
.
5.小明准备用26元钱买火腿肠和方便面,已知一根火腿肠2元,一盒方便面3元,他买了5盒方便面,还可以买多少根火腿肠?
6.小华用最小刻度是1厘米的刻度尺,测量一本书的长,测得结果是17.5厘米,这0.5厘米是他估计的,并不准确,若设他所测量的书的长为x厘米,那么x应该满足的不等式是什么?
的值,那么x的正整数解是
.
5.小明准备用26元钱买火腿肠和方便面,已知一根火腿肠2元,一盒方便面3元,他买了5盒方便面,还可以买多少根火腿肠?
6.小华用最小刻度是1厘米的刻度尺,测量一本书的长,测得结果是17.5厘米,这0.5厘米是他估计的,并不准确,若设他所测量的书的长为x厘米,那么x应该满足的不等式是什么?
比较两个数或两个代数式的大小,可以运用求差法:如果a-b>0,则a>b;如果a-b<0,则a<b.
运用求差法比较大小的一般步骤是:(1)作差;(2)判断差的符号;(3)确定大小.
[例6]设x>y,试比较代数式-(8-10x)与-(8-10y)的大小,如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
[思考与分析]根据求差法的步骤我们先求出两个式子的差,然后再根据已知条件x>y,来判断这个差的符号,从而比较两个代数式的大小.
解:由两式作差得-(8-10x)-[-(8-10y)]=-8+10x+8-10y=10x-10y.
因为x>y,所以10x>10y,即10x-10y>0.
所以-(8-10x)>-(8-10y).
又由题意得-(8-10x)>0,即x>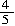 ,所以x最小的正整数值为1.
[例7]有一个三口之家准备在假期出外旅行,咨询时了解到东方旅行社规定:若父母各买一张全票则孩子可以按全票的七折购票;而光明旅行社则规定:三人均可按团体票计价,即按全票的80%收费.若两家旅行社的票价相同,则实际哪家收费较低呢?
[思考与分析]要比较哪家旅行社的收费低,我们可以先用含有未知数的式子表示出两家旅行社需要的费用,然后根据求差法的步骤,求出两个式子的差,再根据已知条件判断这个差的符号即可比较出哪个旅行社的费用低.
解:设这两家旅行社全票的价格为a元,依题意
东方旅行社的收费为2a+70%a=2.7a,
光明旅行社的收费为3a×80%=2.4a.
因为2.7a-2.4a=0.3a>0,
所以实际上光明旅行社的收费较低.
[反思]在解题时我们为什么设这两家旅行社全票的价格为a元呢?因为如果不设的话,我们即使知道用求差法比较大小,也无从下手.
,所以x最小的正整数值为1.
[例7]有一个三口之家准备在假期出外旅行,咨询时了解到东方旅行社规定:若父母各买一张全票则孩子可以按全票的七折购票;而光明旅行社则规定:三人均可按团体票计价,即按全票的80%收费.若两家旅行社的票价相同,则实际哪家收费较低呢?
[思考与分析]要比较哪家旅行社的收费低,我们可以先用含有未知数的式子表示出两家旅行社需要的费用,然后根据求差法的步骤,求出两个式子的差,再根据已知条件判断这个差的符号即可比较出哪个旅行社的费用低.
解:设这两家旅行社全票的价格为a元,依题意
东方旅行社的收费为2a+70%a=2.7a,
光明旅行社的收费为3a×80%=2.4a.
因为2.7a-2.4a=0.3a>0,
所以实际上光明旅行社的收费较低.
[反思]在解题时我们为什么设这两家旅行社全票的价格为a元呢?因为如果不设的话,我们即使知道用求差法比较大小,也无从下手.
[例6] x2与a的和不是正数用不等式表示.
错解及分析: x2+a<0. 对“不是正数”理解不清.x2与a的和是0或负数.
正解: x2+a≤0.
[例7] 求不等式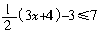 的非负整数解.
错解及分析: 整理得,3x≤16,所以
的非负整数解.
错解及分析: 整理得,3x≤16,所以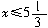 故其非负整数解是1,2,3,4,5.
本例的解题过程没有错误,错在对“非负整数”的理解.
正解:整理得,3x≤16,所以
故其非负整数解是1,2,3,4,5.
本例的解题过程没有错误,错在对“非负整数”的理解.
正解:整理得,3x≤16,所以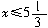 故其非负整数解是0,1,2,3,4,5.
[例8] 解不等式3-5(
故其非负整数解是0,1,2,3,4,5.
[例8] 解不等式3-5(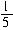 x-2)-4(-1+5x)<0.
错解及分析:去括号,得3-x-2-4+5x<0,即4x<3,所以
x-2)-4(-1+5x)<0.
错解及分析:去括号,得3-x-2-4+5x<0,即4x<3,所以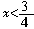 本题一是去括号后各项没有改变符号;二是一个数乘以一个多项式时应该把这个数和多项式的每一项相乘.
正解:去括号得3-x+10+4-20x<0,
即-21x<-17,所以
本题一是去括号后各项没有改变符号;二是一个数乘以一个多项式时应该把这个数和多项式的每一项相乘.
正解:去括号得3-x+10+4-20x<0,
即-21x<-17,所以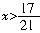 [例9] 解不等式7x-6<4x-9.
错解及分析:移项,得
7x+4x<-9-6,
即11x<-15,所以
[例9] 解不等式7x-6<4x-9.
错解及分析:移项,得
7x+4x<-9-6,
即11x<-15,所以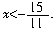 一元一次不等式中移项和一元一次方程中的移项一样,都要改变符号.
正解:移项,得7x-4x<-9+6,
即3x<-3,所以x<-1.
[例10] 解不等式
一元一次不等式中移项和一元一次方程中的移项一样,都要改变符号.
正解:移项,得7x-4x<-9+6,
即3x<-3,所以x<-1.
[例10] 解不等式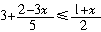 错解及分析:去分母,得
3+2(2-3x)≤5(1+x).
即11x≥2,所以
错解及分析:去分母,得
3+2(2-3x)≤5(1+x).
即11x≥2,所以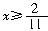 错误的原因是在去分母时漏乘了不含分母的一项“3”.
正解:去分母,得
30+2(2-3x)≤5(1+x).
即11x≥29,所以
错误的原因是在去分母时漏乘了不含分母的一项“3”.
正解:去分母,得
30+2(2-3x)≤5(1+x).
即11x≥29,所以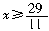 [例11] 解不等式6x-6≤1+7x.
错解及分析:移项,得6x-7x≤1+6.
即-x≤7,所以x<-7.
将不等式-x≤7的系数化为1时,不等式两边同除以-1,不等号没有改变方向,因此造成了错解.
正解:移项,得6x-7x<1+6.
即-x≤7,所以x≥-7.
[例11] 解不等式6x-6≤1+7x.
错解及分析:移项,得6x-7x≤1+6.
即-x≤7,所以x<-7.
将不等式-x≤7的系数化为1时,不等式两边同除以-1,不等号没有改变方向,因此造成了错解.
正解:移项,得6x-7x<1+6.
即-x≤7,所以x≥-7.
[例12] 解关于x的不等式m(x-2)>x-2.
错解: 化简,得(m-1)x>2(m-1),所以x>2.
诊断: 错解默认为m-1>0,实际上m-1还可能小于或等于0.
正解: 化简,得(m-1)x>2(m-1),
① 当m-1>0时,x>2;
② 当m-1<0时,x<2;
③ 当m-1=0时,无解.
[例13] 解不等式(a-1)x>3.
错解: 系数化为1,得x>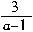 .
诊断: 此题的未知数系数含有字母,不能直接在不等式两边同时除以这个系数,应该分类讨论.
正解: ① 当a-1>0时,x>
.
诊断: 此题的未知数系数含有字母,不能直接在不等式两边同时除以这个系数,应该分类讨论.
正解: ① 当a-1>0时,x>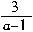 ;
② 当a=1时,0×x>3,不等式无解;
③ 当a-1<0时,x<
;
② 当a=1时,0×x>3,不等式无解;
③ 当a-1<0时,x<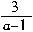 .
[例14] 不等式组
.
[例14] 不等式组 的解集为
.
错解: 两个不等式相加,得 x-1<0,所以x<1.
诊断: 这是解法上的错误,它把解不等式组与解一次方程组的方法混为一谈,不等式组的解法是分别求出不等式组中各个不等式的解集,然后在数轴上表示出来,求得的公共部分就是不等式组的解集,而不能用解方程组的方法来求解
正解: 解不等式组,得
的解集为
.
错解: 两个不等式相加,得 x-1<0,所以x<1.
诊断: 这是解法上的错误,它把解不等式组与解一次方程组的方法混为一谈,不等式组的解法是分别求出不等式组中各个不等式的解集,然后在数轴上表示出来,求得的公共部分就是不等式组的解集,而不能用解方程组的方法来求解
正解: 解不等式组,得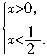 .
在同一条数轴上表示出它们的解集,如图,
.
在同一条数轴上表示出它们的解集,如图,
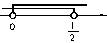 所以不等式组的解集为:0<x<
所以不等式组的解集为:0<x<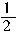 [例15] 解不等式组
[例15] 解不等式组 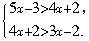 错解: 因为5x-3>4x+2,且4x+2>3x-2,
所以 5x-3>3x-2.
移项,得5x-3x>-2+3.
解得 x>
错解: 因为5x-3>4x+2,且4x+2>3x-2,
所以 5x-3>3x-2.
移项,得5x-3x>-2+3.
解得 x>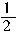 .
诊断: 上面的解法套用了解方程组的方法,是否正确,我们可以在x>
.
诊断: 上面的解法套用了解方程组的方法,是否正确,我们可以在x>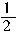 的条件下,任取一个x的值,看是否满足不等式组.如取x=1,将它代入5x-3>4x+2,得2>6(不成立).可知x>
的条件下,任取一个x的值,看是否满足不等式组.如取x=1,将它代入5x-3>4x+2,得2>6(不成立).可知x>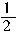 不是原方程组的解集,其造成错误的原因是由原不等式组变形为一个新的不等式时,改变了不等式的解集.
正解: 由5x-3>4x+2,得x>5.
由4x+2>3x-2,得x>-4.
综合x>5和x>-4,得原不等式组的解集为x>5.
不是原方程组的解集,其造成错误的原因是由原不等式组变形为一个新的不等式时,改变了不等式的解集.
正解: 由5x-3>4x+2,得x>5.
由4x+2>3x-2,得x>-4.
综合x>5和x>-4,得原不等式组的解集为x>5.
[例16]解不等式组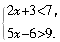 错解:由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以原不等式组的解集为2>x>3.
诊断:由不等式性质可得,2>3,这是不可能的.
正解:由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以原不等式组无解.
[例17] 解不等式
错解:由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以原不等式组的解集为2>x>3.
诊断:由不等式性质可得,2>3,这是不可能的.
正解:由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以原不等式组无解.
[例17] 解不等式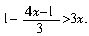 错解:去分母,得3-4x-1>9x.移项,得-4x-9x>1-3合并,得-13x>-2系数化为1,得
错解:去分母,得3-4x-1>9x.移项,得-4x-9x>1-3合并,得-13x>-2系数化为1,得 诊断:本题忽视了分数线的双重作用,去分母时,若分子为多项式,应对其加上括号.
正解: 去分母,得3-(4x-1)>9x去括号,得3-4x+1>9x.移项,得-4x-9x>-1-3合并,得-13x>-4系数化为1,得
诊断:本题忽视了分数线的双重作用,去分母时,若分子为多项式,应对其加上括号.
正解: 去分母,得3-(4x-1)>9x去括号,得3-4x+1>9x.移项,得-4x-9x>-1-3合并,得-13x>-4系数化为1,得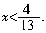 [例18] 若不等式组
[例18] 若不等式组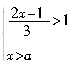 的解集为x>2,则a的取值范围是( ).
A.
a<2 B.
a≤2
C.
a>2 D. a≥2
错解及分析:原不等式组可分为
的解集为x>2,则a的取值范围是( ).
A.
a<2 B.
a≤2
C.
a>2 D. a≥2
错解及分析:原不等式组可分为 得a<2,故选A.
当a=2时,原不等式组变为
得a<2,故选A.
当a=2时,原不等式组变为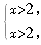 解集也为x>2.
正解:应为a≤2 ,故选B.
[例19]解不等式组
解集也为x>2.
正解:应为a≤2 ,故选B.
[例19]解不等式组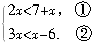 错解:②-①,得不等式组的解集为x<-13.
诊断:错解中把方程组的解法套用到不等式组中.
正解:由不等式2x<7+x得到x<7.
由不等式3x<x-6得到x<-3.
所以原不等式组的解集为x<-3.
错解:②-①,得不等式组的解集为x<-13.
诊断:错解中把方程组的解法套用到不等式组中.
正解:由不等式2x<7+x得到x<7.
由不等式3x<x-6得到x<-3.
所以原不等式组的解集为x<-3.
第四节、思维点拨
第二节、教材解读
1. 常用的不等号有哪些?
常用的不等号有五种,其读法和意义是:
(1)“≠”读作“不等于”,它说明两个量是不相等的,但不能明确哪个大哪个小.
(2)“>”读作“大于”,表示其左边的量比右边的量大.
(3)“<”读作“小于”,表示其左边的量比右边的量小.
(4)“≥”读作“大于或等于”,即“不小于”,表示左边的量不小于右边的量.
(5)“≤”读作“小于或等于”,即“不大于”,表示左边的量不大于右边的量.
2. 如何恰当地列不等式表示不等关系?
(1)找准题中不等关系的两个量,并用代数式表示.
(2)正确理解题目中的关键词语,如:多、少、快、慢、增加了、减少了、不足、不到、不大于、不小于、不超过、非负数、至多、至少等的确切含义.
(3)选用与题意符合的不等号将表示不等关系的两个量的代数式连接起来.
根据下列关系列不等式:a的2倍与b的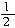 的和不大于3.前者用代数式表示是2a+
的和不大于3.前者用代数式表示是2a+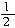 b.“不大于”就是“小于或等于”.
列不等式为:2a+
b.“不大于”就是“小于或等于”.
列不等式为:2a+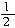 b≤3.
3. 用数轴表示不等式注意什么?
用数轴表示不等式要注意两点:一是边界;二是方向.若边界点在范围内则用实心点表示,若边界点不在范围内,则用空心圆圈表示;方向是对于边界点而言,大于向右画,而小于则向左画.
在同一个数轴上表示下列两个不等式:x>-3;x≤2.
b≤3.
3. 用数轴表示不等式注意什么?
用数轴表示不等式要注意两点:一是边界;二是方向.若边界点在范围内则用实心点表示,若边界点不在范围内,则用空心圆圈表示;方向是对于边界点而言,大于向右画,而小于则向左画.
在同一个数轴上表示下列两个不等式:x>-3;x≤2.
 第三节、错题剖析
第三节、错题剖析
例5、(1)观察下面各式规律:
 ;
;
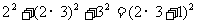 ;
;
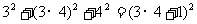 ;
;
……
写出第n行的式子,并证明你的结论。
(2)计算下列各式,你发现了什么规律?
①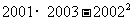 ;②
;②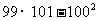 ;③
;③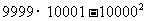
 。
。
例4、(1)两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成一个新的图形。试用不同的方法计算这个图形的面积,你能发现什么?
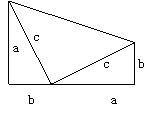
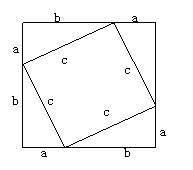
(2)由四个边长分别为a,b,c的直角三角形拼成一个新的图形。试用两种不同的方法计算这个图形的面积,并说说你发现了什么。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com