
若数列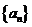 的连续若干项之间满足关系
的连续若干项之间满足关系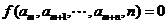 ,由这个递推关系及n个初始值确定的数列,叫做递推数列。它主要给出的是“二层”中连续几项之间的递推关系式(如:
,由这个递推关系及n个初始值确定的数列,叫做递推数列。它主要给出的是“二层”中连续几项之间的递推关系式(如: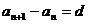 、
、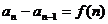 、
、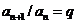 、
、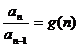 、
、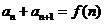 、
、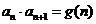 、
、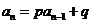 、
、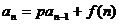 、
、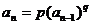 、
、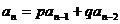 等类型),这是数列的重点、难点问题。求递推数列通项的方法较多,也比较灵活,基本方法如:迭加法、迭乘法、转化为等差、等比数列求通项法、归纳——猜想——证明法等,其中主要的思路是通过转化为等差数列或等比数列来解决问题。
等类型),这是数列的重点、难点问题。求递推数列通项的方法较多,也比较灵活,基本方法如:迭加法、迭乘法、转化为等差、等比数列求通项法、归纳——猜想——证明法等,其中主要的思路是通过转化为等差数列或等比数列来解决问题。
4. 给定初始条件和递推关系,有时不一定能求出通项,却也可以研究它的其他性质。(如取值范围,比较大小,其他等价关系等,无非等与不等两类),这类问题往往有一定的难度。
给定初始条件和递推关系,有时不一定能求出通项,却也可以研究它的其他性质。(如取值范围,比较大小,其他等价关系等,无非等与不等两类),这类问题往往有一定的难度。
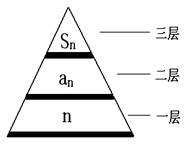
本文主要采用风趣的“楼层式”讲解,更易于理解数列中求通项的问题。将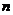 喻为楼的第一层,
喻为楼的第一层,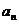 喻为楼的第二层,
喻为楼的第二层,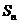 喻为楼的第三层,则数列中
喻为楼的第三层,则数列中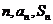 之间的关系式可理解为这三层之间的走动关系,那么我们可以用爬楼层的方式理解
之间的关系式可理解为这三层之间的走动关系,那么我们可以用爬楼层的方式理解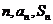 之间的相互转化关系-----我亲切地称它为“楼层式”的转化方式。
之间的相互转化关系-----我亲切地称它为“楼层式”的转化方式。
3.给定初始条件和递推关系往往可以用演绎(推导)的方法求出它的通项公式,其最主要的思想方法是生成、转化、叠代。
2.给出递推关系求通项,有时可以用归纳,猜想,证明的思路;而证明型的问题用数学归纳法往往是一种比较简单的方法;而给出铺垫(转化后的数列)的问题常常可以用证明(变换,待定系数法等)处理,一般难度不大。
例7:已知数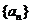 的递推关系为
的递推关系为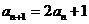 ,且
,且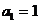 求通项
求通项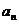 。
。
解:∵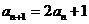 ∴
∴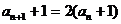 令
令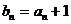 则辅助数列
则辅助数列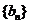 是公比为2的等比数列
是公比为2的等比数列
∴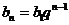 即
即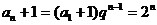 ∴
∴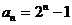
例5.
在数列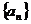 中,
中,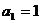 ,
,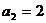 ,
,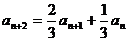 ,求
,求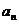 。
。
解析:在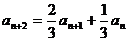 两边减去
两边减去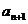 ,得
,得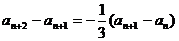
∴ 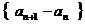 是以
是以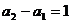 为首项,以
为首项,以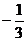 为公比的等比数列,∴
为公比的等比数列,∴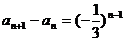 ,由累加法得
,由累加法得
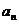 =
=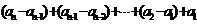 =
=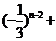
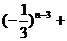 …
…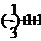 =
=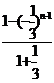 =
=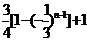 =
= 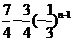
例8: 已知数列{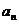 }中
}中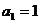 且
且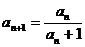 (
(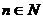 ),,求数列的通项公式。
),,求数列的通项公式。
解:∵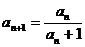 ∴
∴ 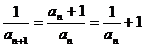 , 设
, 设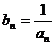 ,则
,则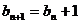
故{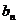 }是以
}是以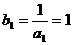 为首项,1为公差的等差数列 ∴
为首项,1为公差的等差数列 ∴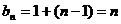 ∴
∴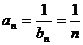
点评:这种方法类似于换元法, 主要用于已知递推关系式求通项公式。
趣谈数列的通项问题及其思维方式
1.递推关系的形成:直接给出,函数给出,解析几何给出,应用问题给出,方程给出。
例6:设数列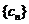 的各项是一个等差数列与一个等比数列对应项的和,若c1=2,c2=4,c3=7,c4=12,求通项公式cn
的各项是一个等差数列与一个等比数列对应项的和,若c1=2,c2=4,c3=7,c4=12,求通项公式cn
解:设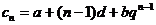

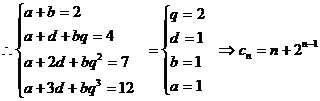
例6. 已知数列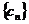 中,
中,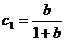 ,
,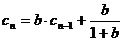 ,
,
其中b是与n无关的常数,且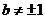 。求出用n和b表示的an的关系式。
。求出用n和b表示的an的关系式。
解析:递推公式一定可表示为
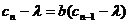 的形式。由待定系数法知:
的形式。由待定系数法知: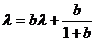
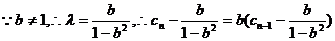

故数列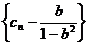 是首项为
是首项为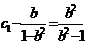 ,公比为
,公比为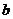 的等比数列,故
的等比数列,故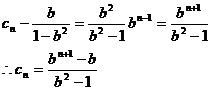
点评:用待定系数法解题时,常先假定通项公式或前n项和公式为某一多项式,一般地,若数列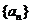 为等差数列:则
为等差数列:则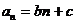 ,
,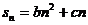 (b、c为常数),若数列
(b、c为常数),若数列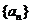 为等比数列,则
为等比数列,则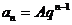 ,
,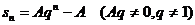 。
。
例5:已知下列两数列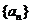 的前n项和sn的公式,求
的前n项和sn的公式,求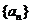 的通项公式。(1)
的通项公式。(1)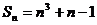 。 (2)
。 (2)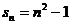
解: (1)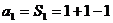
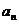 =
=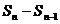 =
=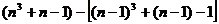 =3
=3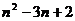
此时,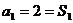 。∴
。∴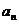 =3
=3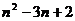 为所求数列的通项公式。
为所求数列的通项公式。
(2)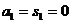 ,当
,当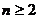 时
时 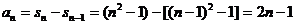
由于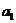 不适合于此等式 。 ∴
不适合于此等式 。 ∴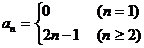
点评:要先分n=1和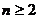 两种情况分别进行运算,然后验证能否统一。
两种情况分别进行运算,然后验证能否统一。
例4:在数列{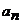 }中,
}中,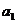 =1,
(n+1)·
=1,
(n+1)·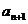 =n·
=n·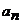 ,求
,求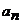 的表达式。
的表达式。
解:由(n+1)·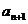 =n·
=n·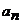 得
得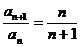 ,
,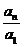 =
=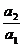 ·
·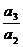 ·
·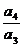 …
…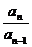 =
=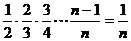 所以
所以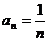
例4. 已知数列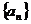 中,
中,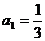 ,前
,前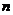 项和
项和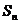 与
与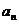 的关系是
的关系是 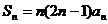 ,试求通项公式
,试求通项公式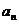 。
。
解析:首先由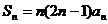 易求的递推公式:
易求的递推公式: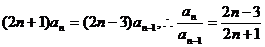
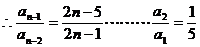 将上面n—1个等式相乘得:
将上面n—1个等式相乘得:
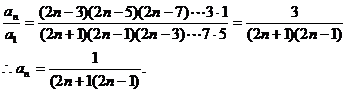
点评:一般地,对于型如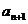 =
=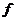 (n)·
(n)·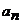 类的通项公式,当
类的通项公式,当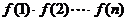 的值可以求得时,宜采用此方法。
的值可以求得时,宜采用此方法。
例3:已知数列6,9,14,21,30,…求此数列的一个通项。
解 易知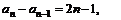 ∵
∵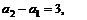
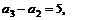
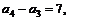 ……
……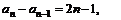
各式相加得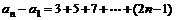 ∴
∴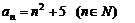
点评:一般地,对于型如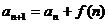 类的通项公式,只要
类的通项公式,只要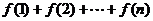 能进行求和,则宜采用此方法求解。
能进行求和,则宜采用此方法求解。
例4. 若在数列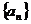 中,
中,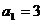 ,
,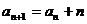 ,求通项
,求通项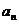 。
。
解析:由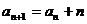 得
得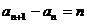
 ,所以
,所以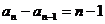 ,
,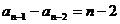 ,…,
,…,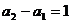 ,
,
将以上各式相加得: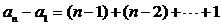 ,又
,又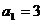 所以
所以 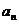 =
=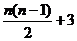
例2: 已知数列{an}是公差为d的等差数列,数列{bn}是公比为q的(q∈R且q≠1)的等比数列,若函数f (x) = (x-1)2,且a1 = f (d-1),a3 = f (d+1),b1 = f (q+1),b3 = f (q-1),(1)求数列{ a n }和{ b n }的通项公式;
解:(1)∵a 1=f (d-1) = (d-2)2,a 3 = f (d+1)= d 2,∴a3-a1=d2-(d-2)2=2d=4,
∴d=2,∴an=a1+(n-1)d = 2(n-1);又b1= f (q+1)= q2,b3 =f (q-1)=(q-2)2,
∴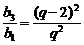 =q2,由q∈R,且q≠1,得q=-2,∴bn=b·qn-1=4·(-2)n-1
=q2,由q∈R,且q≠1,得q=-2,∴bn=b·qn-1=4·(-2)n-1
例1. 等差数列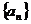 是递减数列,且
是递减数列,且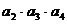 =48,
=48,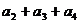 =12,则数列的通项公式是( )
=12,则数列的通项公式是( )
(A) 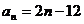 (B)
(B) 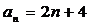 (C)
(C) 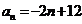 (D)
(D) 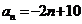
解析:设等差数列的公差位d,由已知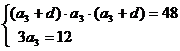 ,
,
解得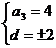 ,又
,又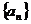 是递减数列, ∴
是递减数列, ∴
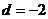 ,
,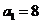 ,∴
,∴ 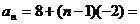
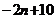 ,故选(D)。
,故选(D)。
例2. 已知等比数列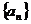 的首项
的首项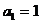 ,公比
,公比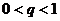 ,设数列
,设数列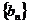 的通项为
的通项为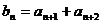 ,求数列
,求数列
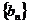 的通项公式。
的通项公式。
解析:由题意,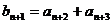 ,又
,又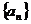 是等比数列,公比为
是等比数列,公比为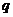
∴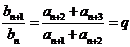 ,故数列
,故数列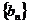 是等比数列,
是等比数列,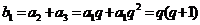 ,∴
,∴ 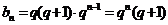
点评:当已知数列为等差或等比数列时,可直接利用等差或等比数列的通项公式,只需求得首项及公差公比。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com