6、在化合物C₄H₁₁N的分子中N原子以三个单键与其它原子连接，则该化合物含有的同分异构体数目是

　　 A．6种　　　　　 B．7种　　　　　 C．8种　　　　　　 D．9种

5、盐酸洛派丁胺俗称易蒙停，它是一种新型的止泻药，适用于各种急慢性腹泻的治疗，其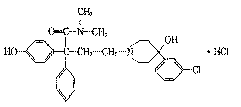结构简式如图：下列说法正确的是

A．易蒙停的分子式为C₂₉H₃₃Cl₂N₂O₃

B．向易蒙停溶液中加入FeCl₃溶液，溶液

显紫色

　 C．1mol易蒙停最多只能与lmolNaOH发生反应

D．lmol易蒙停最多能与3mol溴水发生反应

4、燃烧相同质量的下列有机物，耗氧量最多的是

　A．CH₄　　　　　　 B．C₂H₄　　　　　　 C．C₆H₆　　　　　 D．C₃H₄

3、下列5种有机化合物中，能够发生酯化、加成和氧化三种反应类型的是

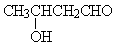① CH₂＝CHCOOH　 ② CH₂＝CHCOOCH₃　 ③ CH₂＝CHCH₂OH　 ④ CH₃ CH₂CH₂OH　

⑤

A．①③④　 　　　　B．①③⑤　　　　 C．②④⑤　　　　 D．①②⑤

2、下列有机物中密度比水大的是

　 A．汽油　　　　　 B．硬脂酸　　　　 C．硝基苯　　　　　 D．乙酸乙酯

1、有机物　　　　　　　　　　 的正确命名为

A．3，3，4-三甲基-己烷　 　　　　　　　　B．3，3-二甲基-4-乙基戊烷

C．3，4，4-三甲基己烷　　　　　　　　　 D．3，3，4-三甲基己烷

2.该怎样追根究底？

总之一句话，要像小孩那样打破沙锅问到底。

小孩子总是爱问一些问题，一直问到自己烦了，父母也烦了为止。

“爸爸！那是什么呀？”

“是交通事故危险指示牌。”

“什么意思呀？”

“就是说如果跑得太快了就会出事故。”

“事故是什么？”

“车子撞了，人受伤了就叫事故！”

“嗯……是这样啊！那危险是什么呢？”

一直这样问下去的话，只能用一些5岁小孩能听懂的话去解释，甚至有时候根本就不会

结束。连续被问20个左右这样的问题之后，大人们恐怕就要说：“哎呀！小孩子不用知道那么多！长大以后就都知道了！”

但如果没有这种提问的过程，小孩子是无法健康成长的，没有一个小孩能略过这一过程

长大成人。

数学学习也是一样。

大部分学生在学习的时候，即使有不懂的东西也只是忽略过去，或者简单地问一下就算

了，更不会为了解决自己不懂的问题而去翻看低年级的教材。你很难看到一个初中生拿着小学的辅导书努力地练习加减法，而问题恰恰就在这儿。

数学是一门如果基础打不好，后面的内容就绝对无法学好的科目。如果基础不够坚实，

在上面建造什么样的房子都很容易就会倒塌。所以，一直要追到源头，弄明白不懂的地方到底在哪里。

不懂的东西就要打破沙锅问到底，直到把老师问烦了为止！这就是对基础追根究底式补

习的核心所在。

该怎样学？

我们来举一个例子。

用英英词典学英语的时候，不认识的单词都是用英语来解释的，而解释中又会有不认识

的单词。然后再用英英词典去查那个单词，它的解释中又会有不认识的单词……这样反复查下去的话，一定会遇到以最简单的、自己全都认识的单词组成的解释，然后就可以从那儿再一点点地逆推上去学习单词。

以这种方式学习单词一段时间以后，到一定的时候，用英语解释的句子中几乎就不会有

什么不认识的单词了。

所谓对基础追根究底式的补习，就是要像这样把自己不懂的基础内容的根源找出来进行

学习。

高中学习二次函数时，如果一次函数的内容还没有弄清楚(做几道初中水平的题目就可

以知道是否已经弄清楚了)，就要回头找到初中的一次函数那个单元。如果对一次函数中正比和反比的基本关系还搞不太清楚，就要再去找初一时学过的内容。就这样一直找下去，总会找到不懂的东西的根源。

之后就从那儿开始，整理内容，通过做一些例题，来重新掌握一下自己不懂部分的基本

概念。然后再解答一些相关的题目，一个阶段一个阶段地学下去。运算能力较弱的初中生要努力做一些小学的题目，可不要死充面子地光学些初中的东西，最后却落得个丢脸的下场……对基础追根究底式的补习可以与任何其他部分的学习一并进行。在学习教科书或者辅导书时，可以既追根究底地补习，同时又照顾进度。特别是自己一个人学习的时候，为了能够把根源找出来，不妨试着去自问自答。所以，要常常把低年级的教科书或辅导书放在身边，随时学习。如果自我感觉对小学阶段学习的内容较有自信，那就把初中的教科书(辅导书)放在身边，现在学习的内容中一旦有搞不懂的问题，就要去翻找查看。如果可以得到其他人的帮助，就要一直问到找出自己不懂的问题的根源为止，也就是直到连一点点的疑问也没有为止……

为了完成对基础追根究底式的补习，一定要具备以下心态：

l　　　 坦率承认自己无知！

l　　　 敢于厚着脸皮带上低年级的辅导书！

l　　　 就算挨打，对不太清楚的问题也绝不马马虎虎一带而过，而要坚持追问到底！

l　　　 即使是因为自己耽误了进度(当然一个人学习的话就无所谓了)，对朋友也毫无愧疚！

也许刚开始看低年级辅导书会有些不自在，怕被别人看见觉得不好意思，不仅如此，与其他部分的学习同时进行时，起初见效不是很快，就更容易产生想要放弃的念头。但以这种方式学习下去的话，随着进度的推进，你会感到不懂的东西在渐渐减少。之后没有多久，在学习中连基础的东西都不知道的情况就再也没有了。此后，进度也会加快，哪怕只学一点儿，对其理解的程度也会更深一些。如果到了这种程度，你就会觉得数学其实并不难，你也会由此发现自己更上一层楼。即便是以其他部分的学习为中心零星地进行追根究底式的基础补习，只要努力，不出三个月你也能看到它的效果。

该学什么？

在对基础追根究底式的补习中，最应该用心学习的就是基本概念、重要公式、基本题型。

5. 慢吞吞、准确性差　

在我教过的学生中，有很多人明明平时可以得80分的，一到考试却总在60分左右晃荡，结果就变成了一副愁眉苦脸的样子。原因就是本来可以做对的题目做错了好几道。发生这种情况，大部分都是由于缺乏快速准确解题的能力导致的。在观看篮球或者足球比赛时，即使解说员在那儿说，“啊！今天的比赛实在是太精彩了！虽败犹荣！”赛场中失败的一方也绝不会笑，因为只有进了更多球而获胜的运动员们才能拥有胜利奖杯。数学也是如此。足球比赛中的射门就好比数学中的得分，不管解题步骤有多好，如果答案错了还是不能得分。因此，如果想得到与自己的实力相符的分数，在解题的时候能做到准确解答就是很重要的。另外，为了能在规定的时间内全部解答完毕，解题就一定要迅速。

观察一下学习好的学生，你就会发现他们解题大部分都相当快。另外，他们几乎不会有琐碎的运算，也很少在解题的过程中出错。这就是他们和学习不好的学生之间不易察觉的巨大差异。

“啊！我把这个减号错看成加号了！”

“只要还有时间的话，这两道题我肯定都能做出来。”

这些问题在很多时候足以导致考试成绩拉开近10分的差距。“准确、快速”是现在的初、高中生们必须具备的一种学习能力。

怎样才能既准确又快速地解题呢？

验算是准确解题的方法。验算是解题速度快的人独有的一份礼物，因为如果解题过慢，就没有时间去进行验算了。如果解题的时间不是很充足，与其再去做一道难题，还不如多验算几道简单的更为有利，本书将会对其理由进行说明。另外，考虑到那些把验算误以为是做第二遍的学生们，本书还将介绍一种只需解题时间的1/10~1/5、简单易行的验算方法。

默算和熟练是快速解题的方法。之所以说有必要进行默算，是因为脑子总是比手动得快。另外，所谓熟练，就是指对某道题目熟悉，能把它从头到尾快速解答出来。走过几次的路很容易就能找到，因为你对它已经熟悉了。只有把题目练习到熟练的程度，才可能在考试中奏效。刚做完一遍就觉得“嗯！我现在懂了”这种程度是远远不够的，至少也要做到能够把做过的题目从头到尾一气呵成写下来才行。

等熟悉了默算和熟练的方法之后，往往就会出现脑比手快的现象。如果到了那种程度，不仅做题的时间不会不够用，在进度推进上也会比以前快得多。明明学习过了却总是得不了分，还有比这更委屈的事情吗？只要把我在这儿介绍的方法吃透了，大家就一定能够得到一个与自己实力相符的分数，考试的时候心里也会轻松一些。起码也能得一个对得起自己的分数吧……

4.毫无计划

这是我从一名韩国前乒乓球国家队员那儿听来的故事。

有一个曾在鸡龙山上专攻乒乓球之道的人(人称“鸡龙山道士”)大声叫嚷“我要和刘南奎比赛”(刘南奎系奥运会金牌得主，当时乒乓球队里的老大哥)，开始遭到了拒绝，可是他坚持三天不回家，还爬到附近的大树上大声叫嚷，在他坚持不懈的请求下，国家队最终答应和他打一场比赛。从他热身时紧握乒乓球拍，挥起球拍来虎虎生风的架势来看，似乎不是一般人，“恐怕还真是个‘道士’”。队员们开始有了一点点的紧张，于是先派了一个年龄最小的选手和他比画一下。比赛结果为21∶1，“鸡龙山道士”大败，那1分还是看他太可怜故意让他的。失败后那个人却说：“我要和刘南奎交手！我是专门针对刘南奎进行训练的！”

如果一个人学习的是狗刨式游泳，就算他学的时间再长，恐怕都难以胜过一个曾在小学的校游泳队里训练过的人。如果不对呼吸的方法、手脚的动作等进行系统学习，不管怎样刻苦练习，也很难超出一定的水平。

数学学习也要系统地进行才会有好的效果。

当被问及采用何种学习方法时，很多学生都会异口同声地说“多做几本习题集”，或者“不管会不会，赶紧往下进行”，或者就是“要做有难度的习题集”等等，他们正是以这些事倍功半的方法去学习的。虽然学校也会根据每个人的能力把学生分为上、中、下几个层次来因材施教，但那样分出来的学生水平还是参差不齐的，要做到让他们能够根据自己的水平恰当地学习实际上还是不可能的。对于学校的老师们来说，即便明知道有学生理解不了自己的讲解，也得继续往下讲，这实在是无奈之举。这种不考虑个人能力和水平的学习方式，往往只能得到事倍功半的效果。如果按照这种方法学习，恐怕连一本教科书或一本习题集都难以真正地吃透。还有，即使下了很大的功夫，实力的提高也是很有限的。如果不根据自己的能力和水平制定合适的学习计划，即使在学习上投入了大量的时间，换来的也往往是微不足道的效果。适合自己水平和能力的、系统的学习方法，与不走弯路的、正确的学习方法是不可或缺的。

“以我现在的水平，该从哪儿开始学起呢？”

“应该集中学习什么呢？”

“学完这个之后该学什么呢？”

“到底该学多少才行呢？”

“我怎么检验自己的学习是不是对路呢？”

有必要制定一个包含所有这些疑问的确切答案的、系统的学习计划。即只有看清楚通往

目的地的路，学习起来才会更轻松一些。只有如此，才能迅速提高实力，不致浪费时间。

本书将这种学习计划按照大家的水平分成了5个阶段，并将就具体的学习阶段和方法向大家做出介绍。大家现在处在一个什么样的水平，今后还要再学习些什么，怎样才能达成自己的目标，都将是本书要回答的问题。

本书中所介绍的学习方法都是由我在教学生的过程中最行之有效的东西整理而成的。相信不管是谁，只要稍稍考虑一下，就会意识到只有那样去做才会有效果，同意我的观点。　　　　　　 　没有一个符合个人水平的学习计划，或者不考虑学生水平和能力的学习计划，都会使学习越来越糟糕。