6、在化合物C₄H₁₁N的分子中N原子以三个单键与其它原子连接，则该化合物含有的同分异构体数目是

　　 A．6种　　　　　 B．7种　　　　　 C．8种　　　　　　 D．9种

5、盐酸洛派丁胺俗称易蒙停，它是一种新型的止泻药，适用于各种急慢性腹泻的治疗，其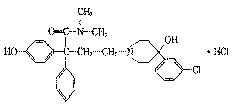结构简式如图：下列说法正确的是

A．易蒙停的分子式为C₂₉H₃₃Cl₂N₂O₃

B．向易蒙停溶液中加入FeCl₃溶液，溶液

显紫色

　 C．1mol易蒙停最多只能与lmolNaOH发生反应

D．lmol易蒙停最多能与3mol溴水发生反应

4、燃烧相同质量的下列有机物，耗氧量最多的是

　A．CH₄　　　　　　 B．C₂H₄　　　　　　 C．C₆H₆　　　　　 D．C₃H₄

3、下列5种有机化合物中，能够发生酯化、加成和氧化三种反应类型的是

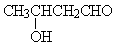① CH₂＝CHCOOH　 ② CH₂＝CHCOOCH₃　 ③ CH₂＝CHCH₂OH　 ④ CH₃ CH₂CH₂OH　

⑤

A．①③④　 　　　　B．①③⑤　　　　 C．②④⑤　　　　 D．①②⑤

2、下列有机物中密度比水大的是

　 A．汽油　　　　　 B．硬脂酸　　　　 C．硝基苯　　　　　 D．乙酸乙酯

1、有机物　　　　　　　　　　 的正确命名为

A．3，3，4-三甲基-己烷　 　　　　　　　　B．3，3-二甲基-4-乙基戊烷

C．3，4，4-三甲基己烷　　　　　　　　　 D．3，3，4-三甲基己烷

8．(2008浙江理)一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球，得到黑球的概率是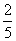；从袋中任意摸出2个球，至少得到1个白球的概率是。

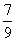　 (Ⅰ)若袋中共有10个球，　　 (i)求白球的个数；

(ii)从袋中任意摸出3个球,记得到白球的个数为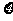,求随机变量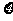的数学期望。

(Ⅱ)求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于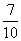。并指出袋中哪种颜色的球个数最少。

历届高考中的概率、分布列解答题精选(仅供理科使用)

7．(2008福建理)某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可继续参加科

　　　 目B的考试.已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书. 现某人参加这项考试，科目A每次考试成绩合格的概率均为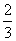，科目B每次考试成绩合格的概率均为.

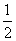假设各次考试成绩合格与否均互不影响.　　　　 (Ⅰ)求他不需要补考就可获得证书的概率；

　　　　　 (Ⅱ)在这项考试过程中，假设他不放弃所有的考试机会，记他参加考试的次数为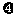，求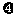的数学期望E.

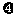5.(2007全国Ⅱ理) 从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件A：“取出的2件产品中至多有1件是二等品”的概率P(A)=0.96

(1)求从该批产品中任取1件是二等品的概率p;

(2)若该批产品共有100件,从中任意抽取2件,x表示取出的2件产品中二等品的件数,求x的分布列

6 (2008湖南理)甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约. 乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设每人面试合格的概率都是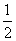，且面试是否合格互不影响. 求：　　　 (Ⅰ)至少有1人面试合格的概率;

(Ⅱ)签约人数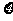的分布列和数学期望.

4.．(2007北京理)(本小题共13分)某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动)．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

(I)求合唱团学生参加活动的人均次数；

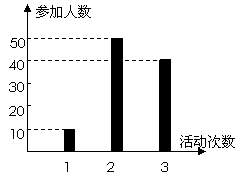(II)从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率．

(III)从合唱团中任选两名学生，用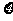表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望．