
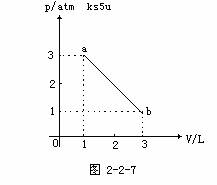
3.如图2-2-7所示,一定质量的理想气体,由状态a沿直线ab变化到状态b.在此过程中 [ ]
A.气体的温度保持不变
B.气体分子平均速率先减小后增大
C.气体的密度不断减小
D.气体必然从外界吸热
2.对于一定质量的理想气体,可能发生的过程是
[ ]
A.气体的压强增大、温度升高,气体对外界做功
B.气体的压强增大、温度不变,气体对外界放热
C.气体的压强减小、温度降低,气体从外界吸热
D.气体的压强减小、温度升高,外界对气体做功
1.如图2-2-6所示,质量不计的活塞把一定质量的理想气体封闭在上端开口的直立圆筒形气缸中,活塞上堆放细砂,活塞处于静止.现在对气体缓慢加热,同时不断取走细砂,使活塞缓慢上升,直到细纱全部取走.则在此过程中 [ ]
A.气体的体积增大,压强减小,对外不做功
B.气体温度可能不变,气体对外做功
C.气体压强减小,内能可能不变
D.气体对外做功,内能可能增加
9.(94年全国理)设{an}是正数组成的数列,其前n项和为Sn,并且对所有自然数n,an与2的等差中项等于Sn与2的等比中项.
(1)写出数列{an}的前三项; (2)求数列{an}的通项公式(写出推证过程);
(3)令bn=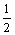
 (n∈N),求:b1+b2+…+bn-n.
(n∈N),求:b1+b2+…+bn-n.
8.(2002年春招试题)已知点的序列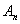 (
(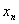 ,0),
,0),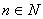 ,其中
,其中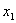 =0,
=0,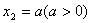 ,A3是线钱A1A2的中点,A4是线段A2A3的中点,…,An是线段
,A3是线钱A1A2的中点,A4是线段A2A3的中点,…,An是线段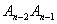 的中点,…。
的中点,…。
(I)写出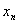 与
与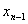 、
、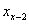 之间的关系式(
之间的关系式(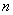 ≥3)
≥3)
(II)设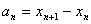 ,计算
,计算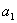 ,
,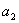 ,
,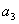 ,由此推测数列{
,由此推测数列{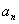 }的通项公式,并加以证明。
}的通项公式,并加以证明。
7.某县位于沙漠地带,人与自然长期进行着顽强的斗争,到2001年底全县的绿化率已达30%。从2002年开始,每年将出现这样的局面,即原有沙漠面积的16%将被绿化,与此同时,由于各种原因,原有绿化面积的4%又被沙化。
(1)设全县面积为1,2001年底绿化面积为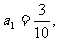 经过
经过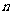 年绿化总面积为
年绿化总面积为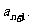
求证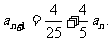
(2)至少需要多少年(年取整数,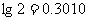 )的努力,才能使全县的绿化率达到60%?
)的努力,才能使全县的绿化率达到60%?
6.数列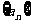 的前
的前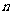 项和
项和 为不等于0,1的常数),求其通项公式
为不等于0,1的常数),求其通项公式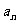
5.根据下面各个数列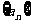 的首项和递推关系,求其通项公式
的首项和递推关系,求其通项公式
⑴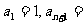
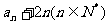
⑵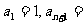
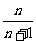
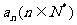
⑶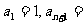
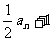
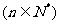
4.设在等比数列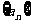 中,
中, 求
求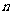 及
及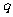
3.若数列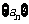 中,
中,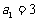 ,且
,且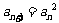
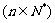 ,则数列的通项
,则数列的通项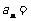 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com