
7.[解析]B. 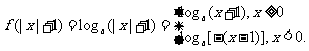 由函数
由函数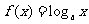 是增函数知,
是增函数知,  .故选B.
.故选B.
[链接高考]本小题主要考查了对数函数的图象与性质,以及分析问题和解决问题的能力.这类试题经常出现,要高度重视.
6.[解析]A. 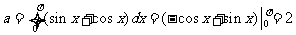 ,二项式
,二项式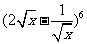 的通项公式为
的通项公式为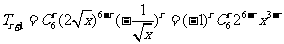 ,令
,令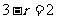 ,得
,得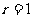 ,故展开式中含
,故展开式中含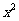 项的系数是
项的系数是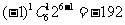 .
.
[链接高考]本小题设计巧妙,综合考查定积分和二项式定理,是一道以小见大的中档题,不可小视.
5.[解析]C.圆心O到直线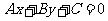 的距离
的距离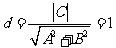 ,所以
,所以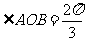 ,,所以
,,所以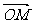 ·
·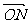 =(·
=(·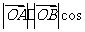
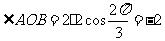 ,故选C.
,故选C.
[链接高考]本题是考察平面几何、向量、解析几何有关知识,预测也是今年是高考考热点,要注意.
4.[解析]B.棱柱的高是4,底面正三角形的高是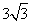 ,设底面边长为
,设底面边长为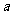 ,则
,则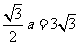 ,
,
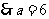 ,故三棱柱体积
,故三棱柱体积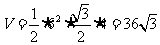 .
.
[链接高考]三视图是高考的新增考点,不时出现在高考试题中,应予以重视.
3.[解析]C.设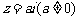 ,则有
,则有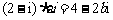 ,即
,即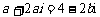 ,即
,即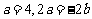 ,解得
,解得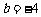 .
.
[链接高考]有关复数的考查,最近五年只是一道选择题,主要考查复数的基本概念和复数的简单运算.
2.[解析]D.解: 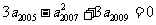 ,即
,即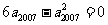 ,
,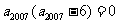 ,由
,由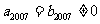 知,
知, 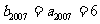 .
.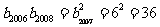 .
.
[链接高考] 本题主要考查了等差数列和等比数列的基本性质. 纵观近几年的高考,基本上是考查两个基本数列的通项公式和前n项和公式的简单运用.这种趋势近几年还会保持. 两类基本数列问题,是高考的热点.
1.[解析]A. 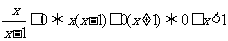 ;
; ,
,
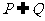 .选A.
.选A.
[链接高考]本题主要考查集合的有关知识,解不等式,以及充要条件等知识.集合是学习其它知识的基础,在高考中时有出现,通常与函数、不等式的知识综合考查,难度不大,基本是送分题.
20. (本小题满分14分)
已知函数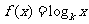 (
(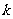 为常数,
为常数,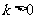 且
且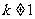 ),且数列
),且数列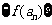 是首项为4,
是首项为4,
公差为2的等差数列.
(Ⅰ)求证:数列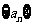 是等比数列;
是等比数列;
(Ⅱ) 若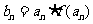 ,当
,当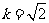 时,求数列
时,求数列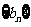 的前
的前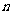 项和
项和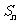 ;
;
(III)若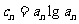 ,问是否存在实数
,问是否存在实数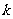 ,使得
,使得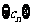 中的每一项恒小于它后面的项?若存在,求出
中的每一项恒小于它后面的项?若存在,求出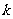 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
19. (本小题满分13分)
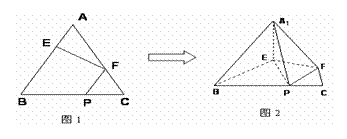 在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到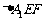 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP; (Ⅱ)求直线A1E与平面A1BP所成角的大小; (III)求二面角B-A1P-F的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com