
1、 书本 P 134 随堂练习 1、2
21.[解析](Ⅰ)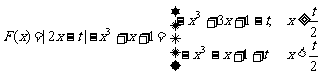
∴ 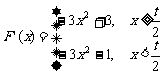 .……………..4分
.……………..4分
由-3x2+3=0 得x1=-1,x2=1,而-3x2-1<0恒成立,
∴ i) 当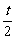 <-1时,F(x)在区间(-∞,-1)上是减函数,
<-1时,F(x)在区间(-∞,-1)上是减函数,
在区间(-1,1)上是增函数,在区间(1,+∞)上是减函数.
ii)
当1>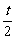 ≥-1时,F(x)在区间(-∞,
≥-1时,F(x)在区间(-∞,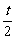 )上是减函数,
)上是减函数,
在区间(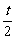 ,1)上是增函数,在区间(1,+∞)上是减函数.
,1)上是增函数,在区间(1,+∞)上是减函数.
iii)
当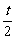 ≥1时,F(x)在(-∞,+∞)上是减函数. .……………..8分
≥1时,F(x)在(-∞,+∞)上是减函数. .……………..8分
(II)由1)可知
i) 当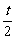 <-1时,F(x)在x=-1处取得极小值-1-t,
<-1时,F(x)在x=-1处取得极小值-1-t,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=-1-t或m=3-t.
ii)
当-1≤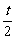 <1,F(x)在x=
<1,F(x)在x=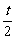 处取值为
处取值为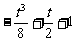 ,
,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=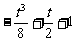 或m=3-t.
或m=3-t.
iii)
当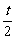 ≥1时,不存在这样的实数m,使得F(x)-m=0恰有两解..……………..14
≥1时,不存在这样的实数m,使得F(x)-m=0恰有两解..……………..14
[链接高考]本题是一道含参数的函数、导数与方程的综合题,需要对参数进行分类讨论. 在新高考中每年有一道导数综合题,同学们应高度重视.
20.[解析](Ⅰ) 证:由题意 ,即
,即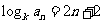 , ……1分
, ……1分
∴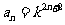 ∴
∴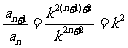 . ……2分
. ……2分
∵常数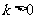 且
且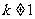 ,∴
,∴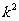 为非零常数,
为非零常数,
∴数列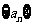 是以
是以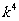 为首项,
为首项,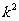 为公比的等比数列. ……3分
为公比的等比数列. ……3分
(II) 解:由(1)知,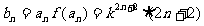 ,
,
当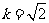 时,
时,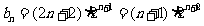 .
…………4分
.
…………4分
∴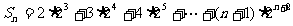 , ①
, ①
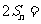
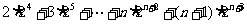 . ② ……5分
. ② ……5分
②-①,得
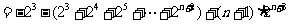
∴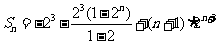
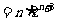 . ……8分
. ……8分
(III) 解:由(1)知,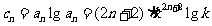 ,要使
,要使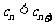 对一切
对一切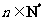 成立,
成立,
即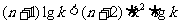 对一切
对一切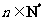 成立.
……9分
成立.
……9分
① 当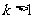 时,
时,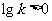 ,
,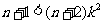 对一切
对一切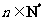 恒成立;……10分
恒成立;……10分
② 当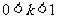 时,
时,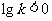 ,
,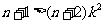 对一切
对一切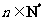 恒成立,只需
恒成立,只需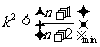 ,……11分
,……11分
∵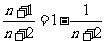 单调递增,∴当
单调递增,∴当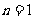 时,
时,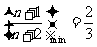 . ……12分
. ……12分
∴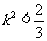 ,且
,且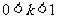 , ∴
, ∴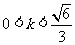 . ……13分
. ……13分
综上所述,存在实数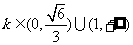 满足条件. ……14分
满足条件. ……14分
[链接高考]本题综合考查数列的基本知识、方法和运算能力,以及分类讨论和化归、转化的思想方法. 错位相减法是数列求和的一种重要方法,备考复习中要引起重视.
19. [解析]不妨设正三角形ABC 的边长为 3 .
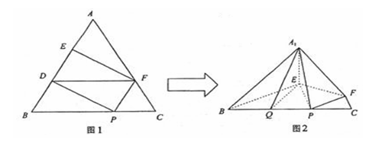
(解法一)(I)在图1中,取BE的中点D,连结DF.
∵AE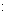 EB=CF
EB=CF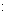 FA=1
FA=1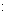 2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
又AE=DE=1,∴EF⊥AD.…………2分
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP.……….4分
(II)在图2中,∵A1E不垂直于A1B,∴A1E是平面A1BP的斜线.
又A1E⊥平面BEP, ∴A1E⊥BP,
从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理).
设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则
∠EA1Q就是A1E与平面A1BP所成的角,…………………6分
且BP⊥A1Q.
在△EBP中,∵BE=BP=2,∠EBP=600,
∴△EBP是等边三角形,∴BE=EP.
又A1E⊥平面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ=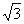 ,
,
又A1E=1,在Rt△A1EQ ,tan∠EA1Q=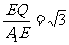 ,∴∠EA1Q=600.
,∴∠EA1Q=600.
所以直线A1E与平面A1BP所成的角为600.…………………8分
(III)在图3中,过F作FM⊥A1P于M,连结QM,QF.
∵CF=CP=1, ∠C=600. ∴△FCP是正三角形,∴PF=1.
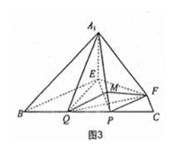 又PQ=
又PQ=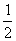 BP=1,∴PF=PQ.
①
BP=1,∴PF=PQ.
①
∵A1E⊥平面BEP,EQ=EF=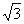 ,
,
∴A1F=A1Q,∴△A1FP≌△A1QP,
从而∠A1PF=∠A1PQ. ②
由①②及MP为公共边知,△FMP≌△QMP,
∴∠QMP=∠FMP=900,且MF=MQ,
从而∠FMQ为二面角B-A1P-F的平面角.……………10分
在Rt△A1QP中,A1Q=A1F=2,PQ=1,∴A1P=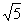 .
.
∵MQ⊥A1P, ∴MQ=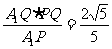 ,∴MF=
,∴MF=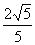 .
.
在△FCQ中,FC=1,QC=2,∠C=600,由余弦定理得QF=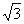 .
.
在△FMQ中,cos∠FMQ=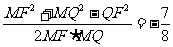 .
.
所以二面角B-A1P-F的余弦值是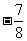 ..……………..13分
..……………..13分
(解法二)(I)同解法一.
(II)建立分别以ED、EF、EA为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A(0,0,1),
B(2,0,0),F(0, 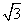 ,0), P (1,
,0), P (1, 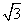 ,0),则
,0),则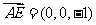 ,
,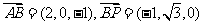 .
.
设平面ABP的法向量为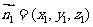 ,
,
由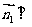 平面ABP知,
平面ABP知,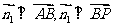 ,即
,即
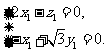 令
令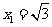 ,得
,得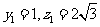 ,
,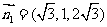 .
.
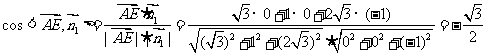 ,
,
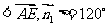 ,
,
所以直线A1E与平面A1BP所成的角为600.
(II) 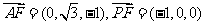 ,设平面AFP的法向量为
,设平面AFP的法向量为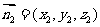 .
.
由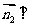 平面AFP知,
平面AFP知,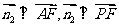 ,即
,即
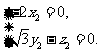 令
令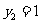 ,得
,得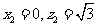 ,
,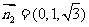 .
.
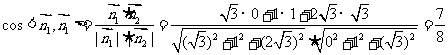 ,
,
所以二面角B-A1P-F的余弦值是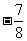 ..……………..13分
..……………..13分
[链接高考]本题主要考查四棱锥的有关知识,直线与平面垂直,直线于平面所成的角,二面角的问题,以及分析问题与解决问题的能力.简单几何体是立体几何解答题的主要载体,特别是棱柱和棱锥.
18. [解析](Ⅰ)由题意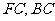 的中垂线方程分别为
的中垂线方程分别为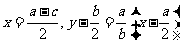 ,
,
于是圆心坐标为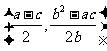 .
…………………………………4分
.
…………………………………4分
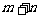 =
=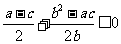 ,即
,即 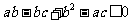 ,
,
即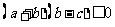 ,所以
,所以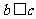 ,于是
,于是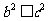 >
>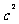 即
即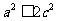 ,
,
所以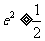 ,即
,即 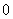 <
<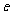 <
<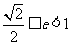 .
………………7分
.
………………7分
(Ⅱ)假设相切, 则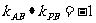 , ………………………………………9分
, ………………………………………9分
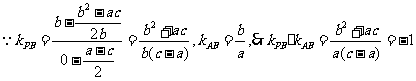 ,……11分
,……11分
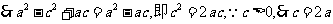 这与
这与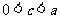 矛盾.
矛盾.
故直线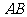 不能与圆
不能与圆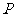 相切. ………………………………………………13分
相切. ………………………………………………13分
[链接高考] 本题主要考查直线与圆、椭圆的位置关系以及分析问题与解决问题的能力.圆锥曲线与圆的综合题经常出现在高考试题中,要引起足够的重视.
17.[解析](Ⅰ)设A队得分为1分的事件为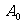 ,
,
∴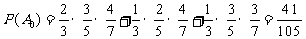 . ………… 4分
. ………… 4分
(Ⅱ)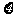 的可能取值为3 , 2 , 1 , 0 ;
的可能取值为3 , 2 , 1 , 0 ;
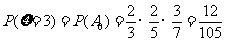 ,
,
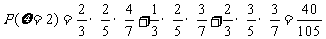
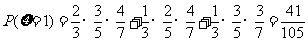 ,
,
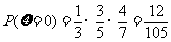 ,
,
∴ 的分布列为:
的分布列为:
 |
0 |
1 |
2 |
3 |
|
P |
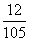 |
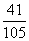 |
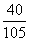 |
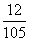 |
………… 10分
于是 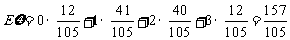 , ……………… 11分
, ……………… 11分
∵  ,
,
∴ 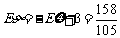 . ………………………
12分
. ………………………
12分
由于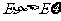 , 故B队比A队实力较强. ……………………… 13分
, 故B队比A队实力较强. ……………………… 13分
[链接高考]本题主要考查的是随机变量的分布列和数学期望问题.这是概率与统计大题考查的主阵地,预计还有可能与函数、导数、方程、数列以及不等式等知识综合考查.
16.[解析](Ⅰ)由题设及正弦定理知: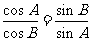 ,得
,得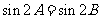
∴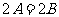 或
或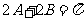 ,即
,即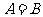 或
或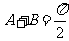
当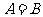 时,有
时,有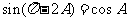 , 即
, 即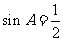 ,得
,得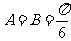 ,
,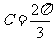 ;
;
当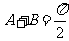 时,有
时,有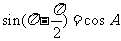 ,即
,即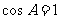 不符题设
不符题设
∴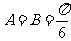 ,
,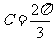 …………………7分
…………………7分
(Ⅱ) 由(Ⅰ)及题设知:
当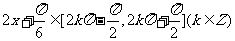 时,
时, 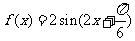 为增函数
为增函数
即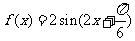 的单调递增区间为
的单调递增区间为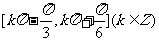 . ………11分
. ………11分
它的相邻两对称轴间的距离为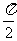 . ………12分
. ………12分
[链接高考] 解决本题的关键是,利用正弦定理把三角形边角问题转化为三角函数问题是解题的关键,三角形与三角函数、向量与三角函数高考考察的热点.
(二)选做题(13-15题,考生只能从中选做两题)
13.(坐标系与参数方程选做题)[解析]1.设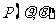 ,
,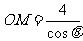 ,
,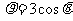 .故P在圆:
.故P在圆: 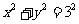 上,而R为直线
上,而R为直线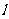 :
: 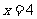 .由图象知,
.由图象知,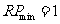 .
.
[链接高考]本小题主要考查直线与圆的极坐标方程的有关知识,以及转化与化归的思想方法.解决本题的关键是将它们转化为直角坐标系下的直线与圆的位置关系问题来处理.
14. (不等式选讲选做题)[解析] .因为
.因为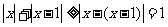 ,所以若不等
,所以若不等
式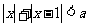 的解集为
的解集为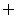 ,则
,则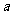 的取值范围是
的取值范围是 .
.
[链接高考]本小题主要考查含绝对值三角不等式的性质,这类问题是高考选做题中的常规题,解题方法要熟练掌握.
15. (几何证明选讲选做题)[解析]28.因为A,M,D,N四点共圆,所以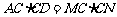 .同理,有
.同理,有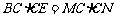 .所以
.所以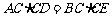 ,即
,即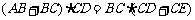 ,所以 AB·CD=BC·DE.
,所以 AB·CD=BC·DE.
设CD=x,则AB=AD- BC-CD=19-4-x=15-x, DE=BE- BC-CD=16-4-x=12-x,则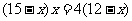 ,即
,即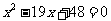 ,解得
,解得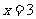 或
或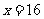 (舍).
(舍).
AE=AB+ DE- BD=19+16-7=28.
[链接高考]本小题主要考查两圆的位置关系,以及相交弦定理的有关知识,分析问题和解决问题的能力,以及转化与化归的思想方法.
(一)必做题(9-12题)
9.[解析]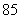 ;
;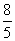 .
由茎叶图知,去掉一个最高分93和一个最低分79后,所剩数据84,84,86,84,87的平均数为
.
由茎叶图知,去掉一个最高分93和一个最低分79后,所剩数据84,84,86,84,87的平均数为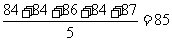 ;方差为
;方差为
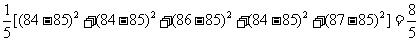 .
.
[链接高考]茎叶图、平均数和方差属于统计部分的基础知识,也是高考的新增内容,考生应引起足够的重视,确保稳拿这部分的分数.
10.[解析]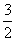 .当
.当 时,
时, 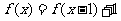 ,故
,故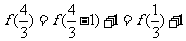
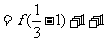
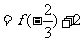
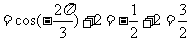 .
.
[链接高考]本题主要考查分段函数,函数的周期性,三角函数的求值等.有关函数方程问题时常出现在高考试题中,考生应该进行专题研究.
11. 由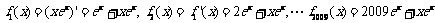 .
.
[链接高考]读懂流程图是高考对这部分内容的最基本的要求,也是最高考常见的题型.本题是把导数的运算与流程图结合在一起的综合题.
12.[解析]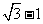 .由
.由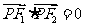 知,
知,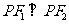 .由
.由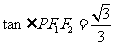 知,
知, 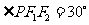 .则
.则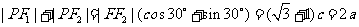 ,即
,即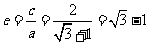 .
.
[链接高考]本题是有关椭圆的焦点三角形问题,却披上了平面向量的外衣,实质是解三角形知识的运用.
8.[解析]D.设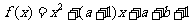 ,则方程
,则方程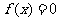 的两实根
的两实根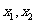 满足
满足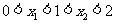 的
的
充要条件是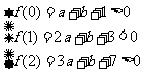 ,作出点
,作出点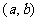 满足的可行域为Δ
满足的可行域为Δ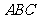 的内部,其中点
的内部,其中点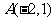 、
、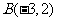 、
、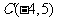 ,
,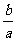 的几何意义是Δ
的几何意义是Δ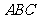 内部任一点
内部任一点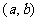 与原点
与原点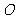 连线的斜率,而
连线的斜率,而 ,
, ,
,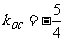 作图,易知
作图,易知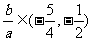 .
.
[链接高考]本小题是一道以二次方程的根的分布为载体的线性规划问题,考查化归转化和数形结合的思想,能力要求较高.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com