
18、解:(Ⅰ) 由三视图可知,四棱锥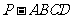 的底面是边长为1的正方形,
的底面是边长为1的正方形,
侧棱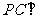 底面
底面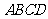 ,且
,且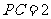 .
…3分
.
…3分
 ∴
∴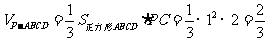 ,
,
即四棱锥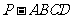 的体积为
的体积为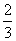 .
…………5分
.
…………5分
(Ⅱ) 连结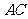 、
、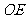 ,
,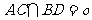
∵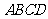 是正方形,
是正方形,
∴ 是
是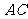 的中点,且
的中点,且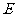 是
是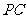 的中点
的中点
∴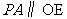
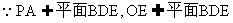
∴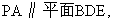 …………9分
…………9分
(Ⅲ)不论点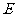 在何位置,都有
在何位置,都有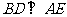 .
…………10分
.
…………10分
证明如下:∵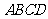 是正方形,∴
是正方形,∴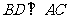 .
.
∵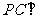 底面
底面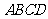 ,且
,且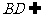 平面
平面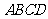 ,∴
,∴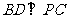 .
.
又∵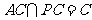 ,∴
,∴ 平面
平面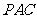 .
.
∵不论点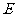 在何位置,都有
在何位置,都有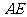
 平面
平面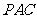 .
.
∴不论点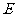 在何位置,都有
在何位置,都有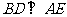 . …………14分
. …………14分
17.[答案]:(I)基本事件总数为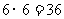 ,
,
若使方程有两个不等实根,则 ,即
,即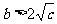 。
。
当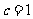 时,b=3, 4, 5, 6; 当
时,b=3, 4, 5, 6; 当 时,
时,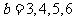 ; 当
; 当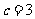 时,
时,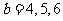 ;
;
当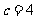 时,b=5, 6; 当
时,b=5, 6; 当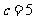 时,
时,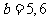 ; 当
; 当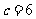 时,
时,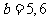 ,
,
目标事件个数为4+4+3+2+2+2=17. 因此方程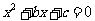 有两个不等实根的概率为
有两个不等实根的概率为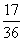 .
.
(II) 若方程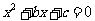 有两个相等实根,则
有两个相等实根,则 ,即
,即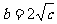 。
。
又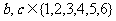 ,所有满足该条件的b,c只有两组,当
,所有满足该条件的b,c只有两组,当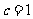 时,b=2;当
时,b=2;当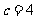 时,b=4;
时,b=4;
因此方程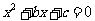 有两个相等实根的概率为
有两个相等实根的概率为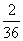 .
.
所以,方程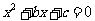 没有实根的概率是
没有实根的概率是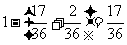
16、
解:(Ⅰ)因为 ,
,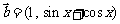 ,所以
,所以
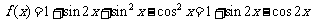 …………………………4分
…………………………4分
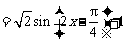 ……………………………………………………..6分
……………………………………………………..6分
因此,当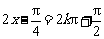 ,即
,即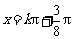 (
(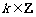 )时,
)时,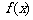 取得最大值
取得最大值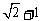 ;…8分
;…8分
(Ⅱ)由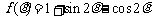 及
及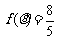 得
得 ,两边平方得
,两边平方得
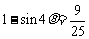 ,即
,即 .……………………………………………14分
.……………………………………………14分
11、8;12、-4;13、9;14、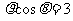 15、
15、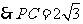
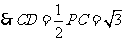
CBDAC,BDCAC
20. (本小题共14分)
某厂为适应市场需求,提高效益,特投入98万元引进先进设备,并马上投入生产,第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元。请你根据以上数据,解决下列问题:
(Ⅰ)引进该设备多少年后,开始盈利?
(Ⅱ)引进该设备若干年后,有两种处理方案:第一种:年平均盈利达到最大值时,以26万元的价格卖出;第二种:盈利总额达到最大值时,以8万元的价格卖出,哪种方案较为合算?请说明理由.
周考(3)答案:
19.(本小题共14分)
已知函数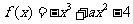 (
(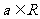 ).
).
(Ⅰ)若函数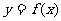 的图象在点
的图象在点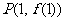 处的切线的倾斜角为
处的切线的倾斜角为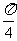 ,求
,求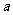 的值;
的值;
(Ⅱ)若存在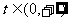 ,总有
,总有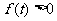 ,求
,求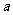 的取值范围.
的取值范围.
18.(本小题共14分)
已知四棱锥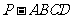 的三视图如下图所示,
的三视图如下图所示,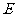 是侧棱
是侧棱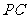 上的动点.
上的动点.
(Ⅰ) 求四棱锥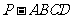 的体积;
的体积;
(Ⅱ) 若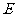 是
是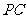 的中点,求证
的中点,求证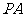 ∥平面
∥平面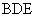

(Ⅲ) 是否不论点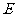 在何位置,都有
在何位置,都有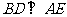 ?证明你的结论.
?证明你的结论.

17、.设方程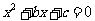 的系数
的系数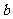 和
和 分别是先后抛掷一枚骰子得到的点数.
分别是先后抛掷一枚骰子得到的点数.
(Ⅰ)求方程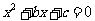 有两个不等实根的概率;
有两个不等实根的概率;
(Ⅱ)求方程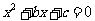 没有实根的概率;
没有实根的概率;
16.(本小题满分12分)已知向量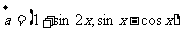 ,
, ,函数
,函数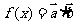 .
.
(1)求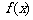 的最大值及相应的
的最大值及相应的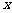 的值;
的值;
(2)若 ,求
,求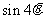 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com