
4.教学重点:
(1)认识轴对称图形的特点,建立轴对称图形的概念;
(2)准确判断生活中哪些事物是轴对称图形。
3.教学目的:
根据大纲的要求和教材的特点,结合六年级学生的实际水平,本节课可确定如下教学目标:
(1)通过观察操作,认识轴对称图形的特点,掌握轴对称图形的概念。
(2)能准确判断哪些事物是轴对称图形。
(3)能找出轴对称图形的对称轴。
(4)通过实验,培养学生的抽象思维和空间想象能力。
(5)结合教材和连系生活实际培养学生的学习兴趣和热爱生活的情感。
2.教材的编写意图:
教材从具体到抽象,从感性到理性,从实践到理论,再用实践检验理论,层次分明,循序渐进地指导学生认识自然界和日常生活中具有轴对称性质的事物,使学生进一步认识前面所学的平面图形的本质特征。
1.说课内容:.

 九年义务教育六年制小学《数学》第十一册第四单元第四小节P121页 122页 轴对称图形。
九年义务教育六年制小学《数学》第十一册第四单元第四小节P121页 122页 轴对称图形。
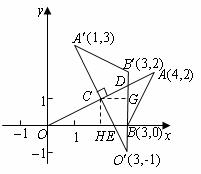
8.[解析]这是一道坐标几何题,中考中的坐标几何题,融丰富的几何图象于一题,包含的知识点较多;代数变换(包括数式变换、方程变换、不等式变换)与几何推理巧妙融合,交相辉映,数形结合思想和方法得到充分运用.本题(2)中的面积的计算是根据旋转不变性,构造全等三角形,将四边形的面积进行转化,这是一种重要的数学思想方法.
[答案]:证明:(1)3.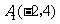 ,
,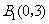
(2)作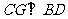 于
于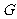 ,
, 轴于
轴于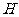 ,
,
 的横坐标相等,
的横坐标相等,
 轴,
轴, 四边形
四边形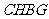 为矩形.
为矩形.
又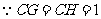 ,
, 矩形
矩形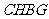 为正方形.
为正方形.
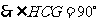 .
.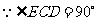 ,
,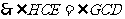 .
.
在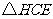 和
和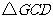 中,
中,

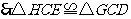 .
.
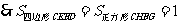 .
.
(3)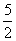 .
.
7.[解析]解决运动型的问题,关键是将其运用过程在头脑当中预演一遍,找准其运用时各个量的变化规律,再动中取静,得到相关量之间的关系.
[答案]解:(1)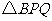 是等边三角形.
是等边三角形.
当 时.
时.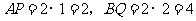 .
.
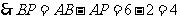 .
.
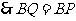 .
.
又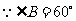 ,
,
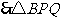 是等边三角形.
是等边三角形.
(2)过 作
作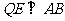 ,垂足为
,垂足为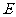 .
.
由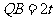 ,得
,得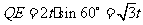 .
.
由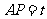 ,得
,得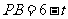 .
.
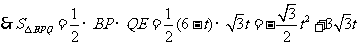 .
.
(3)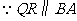 ,
,
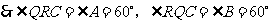 .
.
又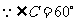 ,
,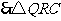 是等边三角形.
是等边三角形.
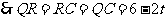 .
.
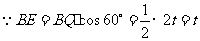 ,
,
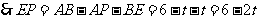 ,
,
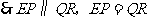 .
.
 四边形
四边形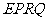 是平行四边形.
是平行四边形.
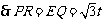 .
.
又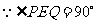 ,
,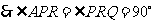 .
.
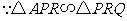 ,
,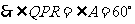 .
.
 ,即
,即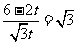 .
.
解得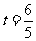 .
.
 当
当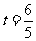 时,
时,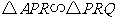
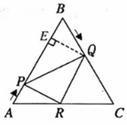
6.[解析]这是一个集几何、代数知识于一体的综合题,既能考查学生的创造性思维品质,又能体现学生的实际水平和应变能力,其解题策略是“动”中求“静”,“一般”中见“特殊”,抓住要害,各个击破.
[答案]解:(1)36;(2)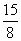 秒;
秒;
(3)当 三点构成直角三角形时,有两种情况:
三点构成直角三角形时,有两种情况:
①当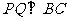 时,设
时,设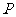 点离开
点离开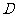 点
点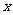 秒,
秒,
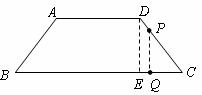
作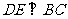 于
于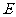 ,
,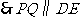 .
.
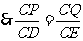 ,
,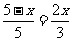 ,
,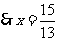 .
.
 当
当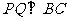 时,
时,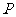 点离开
点离开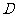 点
点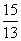 秒.
秒.
②当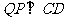 时,设
时,设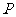 点离开
点离开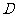 点
点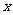 秒,
秒,
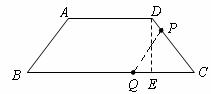
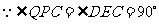 ,
,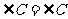 .
.
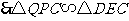 .
.
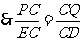 .
.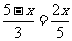 .
.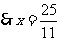 .
.
 当
当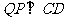 时,点
时,点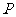 离开点
离开点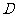
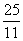 秒.
秒.
由①②知,当 三点构成直角三角形时,点
三点构成直角三角形时,点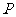 离开点
离开点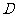
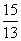 秒或
秒或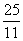 秒.
秒.
5.[解析]该题所蕴涵的知识量较大,并以动态形式,着重考查了四边形、三角形、相似形、平面直角坐标系、二次函数、不等式组等知识点,且解法思路多样化,易于发展学生的各种思维能力。
[答案]解:(1)(4,0),(0,3);
(2) 2,6;
(3) 当0<t≤4时,OM=t.
由△OMN∽△OAC,得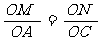 ,
,
∴ ON=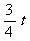 ,S=
,S=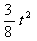 .
.
当4<t<8时,
如图,∵ OD=t,∴ AD= t-4.
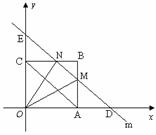
方法一:由△DAM∽△AOC,可得AM=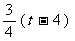 ,∴ BM=6-
,∴ BM=6-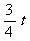 .
.
由△BMN∽△BAC,可得BN=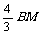 =8-t,∴
CN=t-4.
=8-t,∴
CN=t-4.
S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积
=12-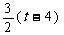 -
-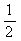 (8-t)(6-
(8-t)(6-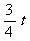 )-
)-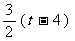
= .
.
方法二:易知四边形ADNC是平行四边形,∴ CN=AD=t-4,BN=8-t.
由△BMN∽△BAC,可得BM=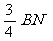 =6-
=6-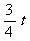 ,∴ AM=
,∴ AM=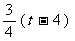 ,以下同方法一.
,以下同方法一.
(4) 有最大值.
方法一:当0<t≤4时,∵ 抛物线S=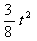 的开口向上,在对称轴t=0的右边,
S随t的增大而增大,
的开口向上,在对称轴t=0的右边,
S随t的增大而增大,
∴ 当t=4时,S可取到最大值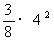 =6;
=6;
当4<t<8时,∵ 抛物线S= 的开口向下,它的顶点是(4,6),∴ S<6.
的开口向下,它的顶点是(4,6),∴ S<6.
综上,当t=4时,S有最大值6.
方法二:
∵ S=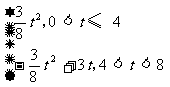
∴ 当0<t<8时,画出S与t的函数关系图像,如图所示.
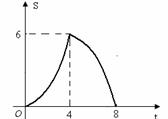
显然,当t=4时,S有最大值6.
4. [答案](1)证明:设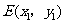 ,
,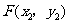 ,
,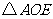 与
与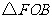 的面积分别为
的面积分别为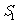 ,
,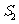 ,
,
由题意得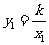 ,
,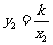 .
.
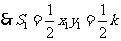 ,
,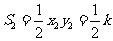 .
.
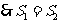 ,即
,即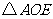 与
与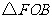 的面积相等.
的面积相等.
(2)由题意知: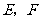 两点坐标分别为
两点坐标分别为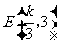 ,
,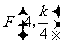 ,
,
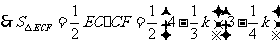 ,
,
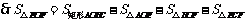
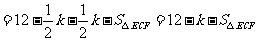
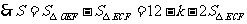
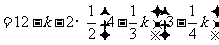
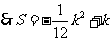 .
.
当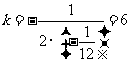 时,
时,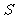 有最大值.
有最大值.
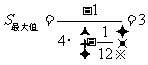 .
.
(3)解:设存在这样的点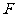 ,将
,将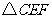 沿
沿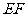 对折后,
对折后,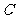 点恰好落在
点恰好落在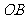 边上的
边上的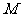 点,过点
点,过点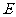 作
作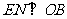 ,垂足为
,垂足为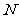 .
.
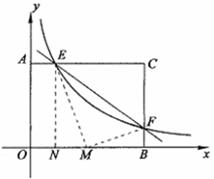
由题意得: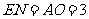 ,
,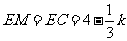 ,
,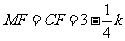 ,
,
 ,
,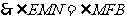 .
.
又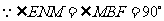 ,
,
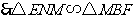 .
.
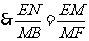 ,
,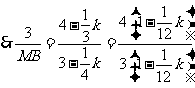 ,
,
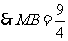 .
.
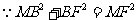 ,
,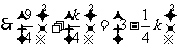 ,解得
,解得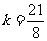 .
.
 .
.
 存在符合条件的点
存在符合条件的点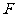 ,它的坐标为
,它的坐标为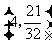 .
.
3.[答案](1)将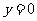 代入
代入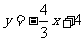 ,得
,得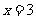 ,
, 点
点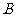 的坐标为
的坐标为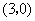 ;
;
将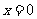 代入
代入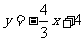 ,得
,得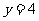 ,
, 点
点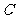 的坐标为
的坐标为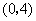 .
.
在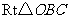 中,
中,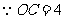 ,
,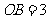 ,
,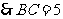 .
.
又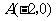 ,
,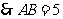 ,
,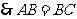 ,
,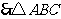 是等腰三角形.
是等腰三角形.
(2)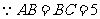 ,故点
,故点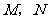 同时开始运动,同时停止运动.
同时开始运动,同时停止运动.
过点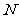 作
作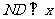 轴于
轴于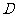 ,
,
则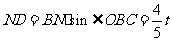 ,
,
①当 时(如图甲),
时(如图甲),
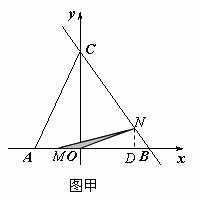
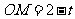 ,
,
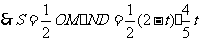
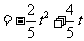 .
.
当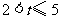 时(如图乙),
时(如图乙),
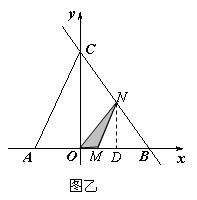
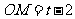 ,
,
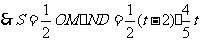
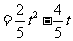 .
.
(注:若将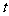 的取值范围分别写为
的取值范围分别写为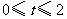 和
和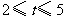 也可以)
也可以)
②存在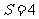 的情形.
的情形.
当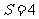 时,
时,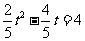 .
.
解得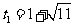 ,
,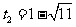 (不合题意,舍去).
(不合题意,舍去).
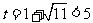 ,故当
,故当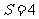 时,
时, 秒.
秒.
③当 轴时,
轴时,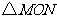 为直角三角形.
为直角三角形.
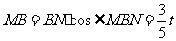 ,又
,又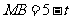 .
.
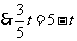 ,
,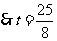 .
.
当点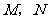 分别运动到点
分别运动到点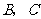 时,
时,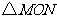 为直角三角形,
为直角三角形,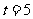 .
.
故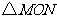 为直角三角形时,
为直角三角形时,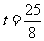 秒或
秒或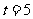 秒.
秒.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com