
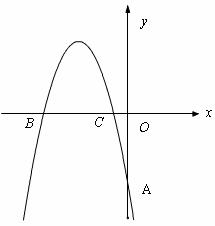
6.(·茂名)如图,在平面直角坐标系中,抛物线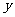 =-
=-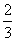

 +
+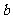
 +
+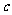 ,经过A(0,-4)、B(
,经过A(0,-4)、B(
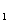 ,0)、 C(
,0)、 C(
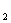 ,0)三点,且
,0)三点,且
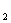 -
-
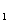 =5.
=5.
(1)求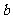 、
、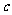 的值;
的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
5.(·恩施自治州)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
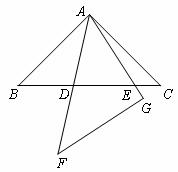

图1
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD +CE
+CE =DE
=DE .
.
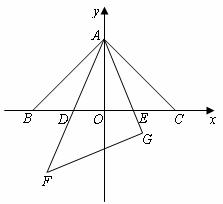

图2
(4)在旋转过程中,(3)中的等量关系BD +CE
+CE =DE
=DE 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
















4.(·益阳) △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
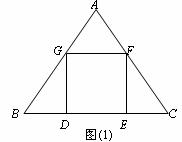

Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出
正方形的边长就能求出BD和CE的长,从而确定D点和
E点,再画正方形DEFG就容易了.
设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
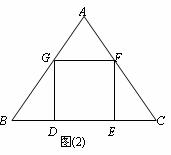

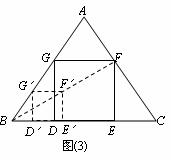
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,
GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.









类型之三 几何与代数相结合的综合题
几何与代数相结合的综合题是初中数学中涵盖广、综合性最强的题型.它可以包含初中阶段所学的代数与几何的若干知识点和各种数学思想方法,还能有机结合探索性、开放性等有关问题;它既突出考查了初中数学的主干知识,又突出了与高中衔接的重要内容,如函数、方程、不等式、三角形、四边形、相似形、圆等.它不但考查学生数学基础知识和灵活运用知识的能力还可以考查学生对数学知识迁移整合能力;既考查学生对几何与代数之间的内在联系,多角度、多层面综合运用数学知识、数学思想方法分析问题和解决问题的能力,还考查学生知识网络化、创新意识和实践能力.
3.(·龙岩市)如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求MC的长及直线DC的解析式.
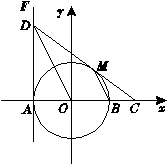











2.(•沈阳市)一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往与A处相距636千米的B地,下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
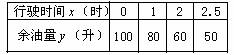

(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y与 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从A处出发行驶4.2小时到达C处,求此时油箱内余油多少升?
(3)在(2)的前提下,C处前方18千米的D处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B地.(货车在D处加油过程中的时间和路程忽略不计)










类型之二 几何类型的综合题
几何综合题考查知识点多、条件隐晦,要求学生有较强的理解能力,分析能力,解决问题的能力,对数学知识、数学方法有较强的驾驭能力,并有较强的创新意识与创新能力. 解决几何型综合题的关键是把代数知识与几何图形的性质以及计算与证明有机融合起来,进行分析、推理,从而达到解决问题的目的.
1.(·安徽省)刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再往A镇参加救灾。一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时。
⑴若二分队在营地不休息,问二分队几小时能赶到A镇?
⑵若二分队和一分队同时赶到A镇,二分队应在营地休息几小时?
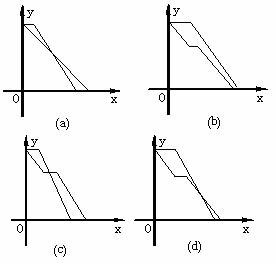
⑶下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义。







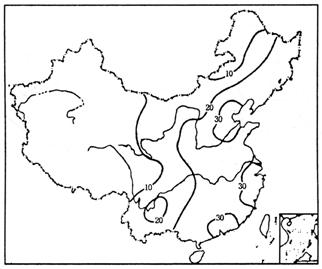
32.读我国某类自然灾害频度(次数)图,回答下列问题。(20分)
(1)此图反映的自然灾害是___________。
A.干旱灾害 B.台风灾害 C.地质灾害 D.寒潮灾害
(2)在我国北方地区,此种灾害最严重的地区是___________。造成此地区灾害严重的原因主要是什么?
(3)针对第(2)题中灾害最严重地区,提出合理化的减灾对策。
31.随着西部大开发,经济发展的同时,生态环境也出现不同程度的问题,根据下图回答:(20分)
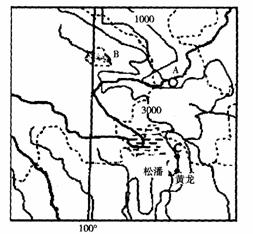
(l)城市A所在省的简称为 ,该省所面临的主要生态环境问题有 。
(2) B湖是 ,试分析近年来该湖面积不断缩小的原因。
(3)在松潘以北地区有我国一块著名的沼泽地,试分析该地区形成沼泽的自然原因。
30、2005年11月我国松花江流域发生严重水污染后,我国迅速向俄罗斯政府作出了污染报告,这说明了
A.环境问题的全球性 B.环境问题的综合性
C.环境问题的积累性 D.环境问题的社会性
湿地与森林、海洋一起并称为全球三大生态系统,被誉为“地球之肾”。每年2月23日为“国际湿地日”。据此回答28-29题:
28.湿地的主要生态功能有
A.涵养水源、保持水土、减轻污染 B.吸烟滞尘,净化空气
C.吸纳一切来自自然和人为的污染物 D.吸收阳光中的紫外线
29.导致我国长江流域湿地面积大量减少的主要原因是
A.气候变暖,水分蒸发 B.工农业废水的大量排放
C.围湖造田,垦荒种粮 D.过度开发,发展旅游业
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com