
1.实际问题向数学问题的转化;
5.解:(Ⅰ)求导得f2(x)=[x2+(b+2)x+b+c]ex..
因b2>4(c-1),故方程f2(x)=0即x2+(b+2)x+b+c=0有两根;
x1=-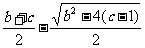 <x2=-
<x2=-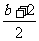
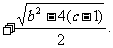
令f′(x)>0,解得x<x1或x>x1;又令f′(x)>0,解得x1<x<x2.
故当xε(-, x1)时,f(x)是增函数,当 xε(x2,+)时,f(x)也是增函数,但当xε(x1 , x2)时,f(x)是减函数.
(Ⅱ)易知f(0)=c,f(u)=b+c,因此
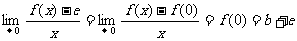 .所以,由已知条件得
.所以,由已知条件得
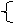 b+e=4
b+e=4
b2≤4(e-1), 因此b2+4b-12≤0.解得-6≤b≤2.
4.解:(I) 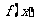 的定义域为(
的定义域为( ,1)
,1)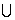 (1,
(1, )
)

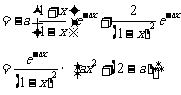
因为 (其中
(其中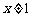 )恒成立,所以
)恒成立,所以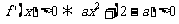
⑴ 当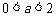 时,
时,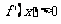 在(
在( ,0)
,0)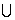 (1,
(1, )上恒成立,所以
)上恒成立,所以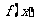 在(
在( ,1)
,1)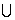 (1,
(1, )上为增函数;
)上为增函数;
⑵ 当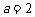 时,
时,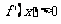 在(
在( ,0)
,0)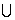 (0,1)
(0,1)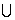 (1,
(1, )上恒成立,所以
)上恒成立,所以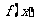 在(
在( ,1)
,1)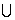 (1,
(1, )上为增函数;
)上为增函数;
⑶ 当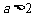 时,
时,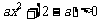 的解为:(
的解为:( ,
,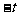 )
)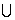 (t,1)
(t,1)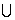 (1,+
(1,+ )
)
(其中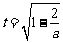 )
)
所以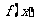 在各区间内的增减性如下表:
在各区间内的增减性如下表:
|
区间 |
( , ,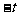 ) ) |
(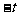 ,t) ,t) |
(t,1) |
(1,+ ) ) |
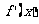 的符号 的符号 |
+ |
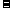 |
+ |
+ |
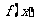 的单调性 的单调性 |
增函数 |
减函数 |
增函数 |
增函数 |
(II)显然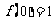
⑴ 当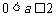 时,
时,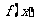 在区间
在区间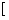 0,1
0,1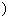 上是增函数,所以对任意
上是增函数,所以对任意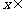 (0,1)都有
(0,1)都有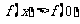 ;
;
⑵ 当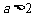 时,
时,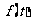 是
是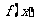 在区间
在区间 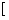 0,1
0,1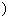 上的最小值,即
上的最小值,即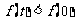 ,这与题目要求矛盾;
,这与题目要求矛盾;
⑶ 若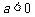 ,
,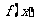 在区间
在区间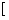 0,1
0,1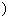 上是增函数,所以对任意
上是增函数,所以对任意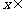 (0,1)都有
(0,1)都有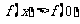 。
。
综合⑴、⑵、⑶ ,a的取值范围为( ,2)
,2)
3.无极值;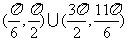 ;
;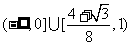
6.解:(Ⅰ)由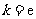 得
得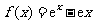 ,所以
,所以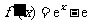 .
.
由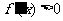 得
得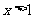 ,故
,故 的单调递增区间是
的单调递增区间是 ,
,
由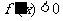 得
得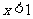 ,故
,故 的单调递减区间是
的单调递减区间是 .
.
(Ⅱ)由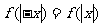 可知
可知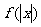 是偶函数.
是偶函数.
于是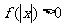 对任意
对任意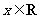 成立等价于
成立等价于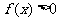 对任意
对任意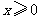 成立.
成立.
由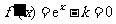 得
得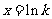 .
.
①当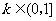 时,
时, .此时
.此时 在
在 上单调递增.
上单调递增.
故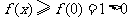 ,符合题意.
,符合题意.
②当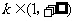 时,
时,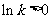 .
.
当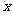 变化时
变化时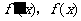 的变化情况如下表:
的变化情况如下表:
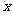 |
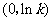 |
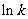 |
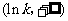 |
 |
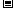 |
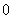 |
 |
 |
单调递减 |
极小值 |
单调递增 |
由此可得,在 上,
上,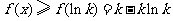 .依题意,
.依题意,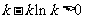 ,又
,又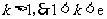 .综合①,②得,实数
.综合①,②得,实数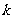 的取值范围是
的取值范围是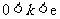 .
.
7.设函数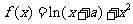
(I)若当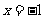 时,
时, 取得极值,求
取得极值,求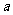 的值,并讨论
的值,并讨论 的单调性;
的单调性;
(II)若 存在极值,求
存在极值,求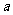 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于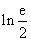 .
.
答案:7.(Ⅰ)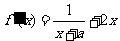 ,依题意有
,依题意有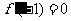 ,故
,故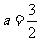 .
.
从而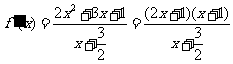 .
.
 的定义域为
的定义域为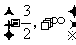 ,当
,当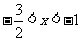 时,
时,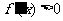 ;
;
当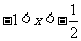 时,
时,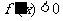 ;当
;当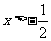 时,
时,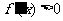 .
.
从而, 分别在区间
分别在区间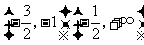 单调增加,在区间
单调增加,在区间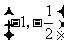 单调减少.
单调减少.
(Ⅱ) 的定义域为
的定义域为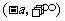 ,
,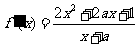 .
.
方程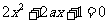 的判别式
的判别式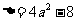 .
.
(ⅰ)若 ,即
,即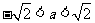 ,在
,在 的定义域内
的定义域内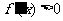 ,故
,故 无极值.
无极值.
(ⅱ)若 ,则
,则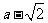 或
或 .
.
若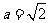 ,
,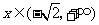 ,
,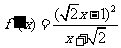 .
.
当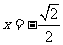 时,
时,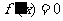 ,当
,当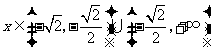 时,
时,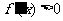 ,所以
,所以 无极值.
无极值.
若 ,
,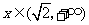 ,
,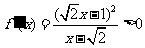 ,
, 也无极值.
也无极值.
(ⅲ)若 ,即
,即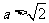 或
或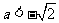 ,则
,则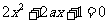 有两个不同的实根
有两个不同的实根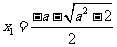 ,
,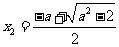 .
.
当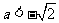 时,
时,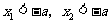 ,从而
,从而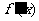 有
有 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.
当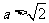 时,
时, ,
, ,
,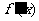 在
在 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知 在
在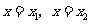 取得极值.
取得极值.
综上, 存在极值时,
存在极值时,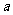 的取值范围为
的取值范围为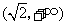 .
.
 的极值之和为
的极值之和为
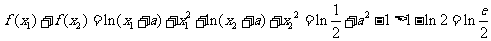
6.已知函数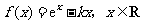
(Ⅰ)若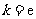 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若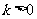 ,且对于任意
,且对于任意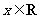 ,
,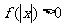 恒成立,试确定实数
恒成立,试确定实数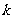 的取值范围;
的取值范围;
5.已知函数f(x)=(x2+bx+c)cx,其中b,c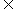 R为常数.
R为常数.
(Ⅰ)若b2>4(c-1),讨论函数f(x)的单调性;
(Ⅱ)若b2<4(c-1),且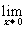
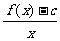 =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.
4.已知函数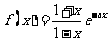 。
。
(Ⅰ)设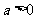 ,讨论
,讨论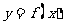 的单调性;
的单调性;
(Ⅱ)若对任意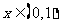 恒有
恒有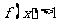 ,求
,求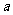 的取值范围
的取值范围
3.已知函数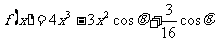 ,其中
,其中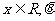 为参数,且
为参数,且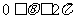 .
.
(1)当时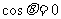 ,判断函数
,判断函数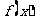 是否有极值;
是否有极值;
(2)要使函数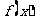 的极小值大于零,求参数
的极小值大于零,求参数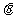 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数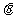 ,函数
,函数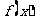 在区间
在区间 内都是增函数,求实数
内都是增函数,求实数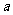 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com