
2.数形结合是解集合问题的常用方法,解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具,将抽象的代数问题具体化、形象化、直观化,然后利用数形结合的思想方法解决;
1.研究集合问题,一定要抓住集合的代表元素,如: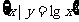 与
与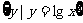 及
及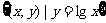
12. (2006江西,21,12分)如图所示,椭圆Q: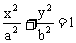 (
(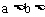 0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点。
0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点。
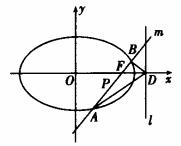
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令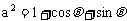 ,
,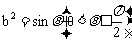 。设轨迹H的最高点和最低点分别为M和N,当
。设轨迹H的最高点和最低点分别为M和N,当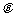 为何值时,△MNF为一个正三角形?
为何值时,△MNF为一个正三角形?
11. (2005江西,21,12分)如图所示,M是抛物线上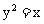 上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB。
上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB。
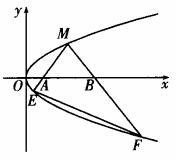
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=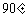 ,求△EMF的重心G的轨迹方程。
,求△EMF的重心G的轨迹方程。
10. 如图所示,平面中两条直线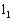 和
和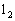 相交于点O,对于平面上任意一点M,若p、q分别是M到直线
相交于点O,对于平面上任意一点M,若p、q分别是M到直线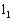 和
和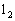 的距离,则称有序非负实数对(p、q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是___________。
的距离,则称有序非负实数对(p、q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是___________。

9. 已知A(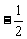 0),B是圆F:
0),B是圆F: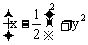 =4(F为圆心)上一动点,线段AB的垂直平分线交BF于点P,则动点P的轨迹方程为______________。
=4(F为圆心)上一动点,线段AB的垂直平分线交BF于点P,则动点P的轨迹方程为______________。
8. 以下四个关于圆锥曲线的命题中
①设A,B为两个定点,k为非零常数,若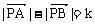 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若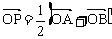 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
③方程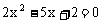 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线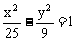 与椭圆
与椭圆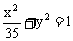 有相同的焦点。
有相同的焦点。
其中真命题的序号为___________(写出所有真命题的序号)。
7. 已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足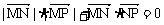 ,则动点P(x,y)的轨迹方程为
,则动点P(x,y)的轨迹方程为
A. 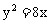 B.
B. 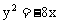 C.
C. 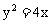 D.
D. 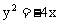
6. 已知两定点A(-2,0),B(1,0),如果动点P满足|PA|=2|PB|,则点P的轨迹所包围的面积等于
A. 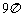 B.
B. 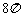 C.
C.  D.
D.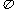
5. 已知点A(-2,0)、B(3,0),动点P(x,y)满足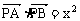 ,则点P的轨迹是
,则点P的轨迹是
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com