3、平面解析几何研究的两个主要问题：

(1)根据已知条件，求出表示曲线的方程；

(2)通过曲线的方程研究曲线的性质．

2、通过研究方程的性质间接地来研究曲线性质，我们把这种借助坐标系研究几何图形的方法叫做坐标法．

[知识梳理]

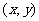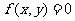1、一般地，如果曲线C上点的坐标都是方程的解，且以方程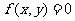的解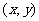为坐标的点都在曲线C上，那么，方程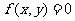叫做曲线C的方程，曲线C叫做方程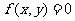的曲线．

曲线的方程及方程的曲线的概念，求曲线方程的几种常见方法；坐标法思想的本质及应用。

2、理解坐标法思想的本质。

1、理解曲线的方程及方程的曲线的概念，掌握求曲线方程的几种常见方法；

解析几何复习：曲线与方程

(七)分布列 走向函数、数列、不等式

例：一群人有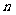个，每个人带甲肝的概率是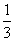，问这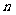个人中，多少人带甲肝的概率最大？

练习：

1． (2006年山东卷)袋中装着标有数学1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用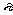表示取出的3个小球上的最大数字，求：取出的3个小球上的数字互不相同的概率；

2．(2006年天津卷)某射手进行射击训练，假设每次射击击中目标的概率为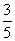，且各次射击的结果互不影响。

(1)求射手在3次射击中，至少有两次连续击中目标的概率(用数字作答)；

(2)求射手第3次击中目标时，恰好射击了4次的概率(用数字作答)；

(3)设随机变量表示射手第3次击中目标时已射击的次数，求的分布列．(理)

3．(2006年全国卷I)A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验。每个试验组由4只小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效。若在一个试验组中，服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组。设每只小白鼠服用A有效的概率为，服用B有效的概率为。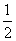

(Ⅰ)求一个试验组为甲类组的概率；　　　　　　　　　　

4．(2006年四川卷)某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、丙三人在理论考核中合格的概率分别为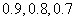；在实验考核中合格的概率分别为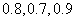，所有考核是否合格相互之间没有影响

(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率；

(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)

5．(2006年北京卷)某公司招聘员工，指定三门考试课程，有两种考试方案.

　　　　 方案一：考试三门课程，至少有两门及格为考试通过；

　　　　 方案二：在三门课程中，随机选取两门，这两门都及格为考试通过.

　　 假设某应聘者对三门指定课程考试及格的概率分别是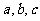，且三门课程考试是否及格相互之间没有影响.分别求该应聘者用方案一和方案二时考试通过的概率；

(六)注意寻求“中间事件”从而沟通基本事件到复杂事件

例：9粒种子分别种在甲、乙、丙3个坑内，每坑3粒，每粒种子发芽的概率为0.5，若一个坑内至少有1粒种子发芽，则该坑不补种；若一个坑内无种子发芽，则补种一次，且补种一个坑需10元，设是补种所需的金额，求，。

(五)待定常数，用方程组求解基本概率

例：甲、乙、丙三台机床各自独立加工同一种零件，已知甲机床加工的零件是一等品而乙机床加工零件不是一等品的概率为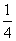，乙机床加工的零件是一等品而丙机床加工零件不是一等品的概率为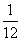，甲丙两台机床加工的零件都是一等品，分别求甲、乙、丙三台机床各自加工的零件是一等品的概率。