
2.已知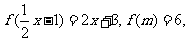 则
则 等于
等于
(A)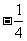 (B)
(B)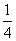 (C)
(C)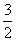 (D)
(D)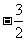
1.设函数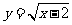 的定义域为集合M,集合N=
的定义域为集合M,集合N=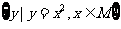 ,则
,则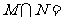
A.M B.N C.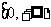 D.
D.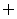
4.顶点(0,2)可能是长轴的端点,也可能是短轴的一个端点,故分两种情况求方程:
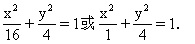
3.点P与一定点F(2,0)的距离和它到一定直线x=8的距离的比是1∶2,求点P的轨迹方程,并说明轨迹是什么图形.

的方程.
作业答案:
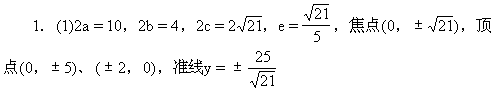
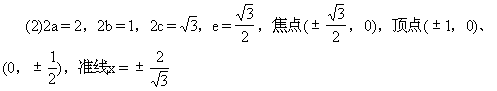
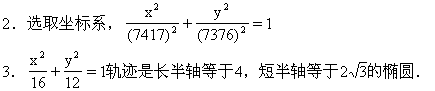
2.我国发射的科学实验人造地球卫星的运行轨道是以地球的中心为一个焦点的椭圆,近地点距地面266Km,远地点距地面1826Km,求这颗卫星的轨道方程.
1.求下列椭圆的长轴和短轴的长、焦距、离心率、各个顶点和焦点坐标、准线方程:
(1)25x2+4y2-100=0,
(2)x2+4y2-1=0.
(五)小结
解法研究图形的性质是通过对方程的讨论进行的,同一曲线由于坐标系选取不同,方程的形式也不同,但是最后得出的性质是一样的,即与坐标系的选取无关.前面我们着重分析了第一个标准方程的椭圆的性质,类似可以理解第二个标准方程的椭圆的性质.布置学生最后小结下列表格:

(四)椭圆的第二定义
1.定义
平面内点M与一个定点的距离和它到一定直线的距离的比是常数

线叫做椭圆的准线,常数e是椭圆的离心率.
2.说明

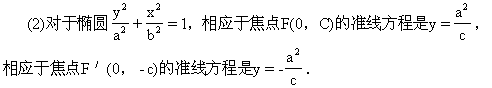
这时还要讲清e的几何意义是:椭圆上一点到焦点的距离和它到准线的距离的比.
(三)应用
为了加深对椭圆的几何性质的认识,掌握用描点法画图的基本方法,给出如下例1.
例1 求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标,并用描点法画出它的图形.
本例前一部分请一个同学板演,教师予以订正,估计不难完成.后一部分由教师讲解,以引起学生重视,步骤是:
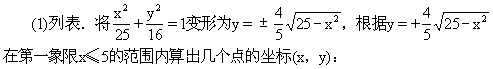

(2)描点作图.先描点画出椭圆在第一象限内的图形,再利用椭圆的对称性就可以画出整个椭圆(图2-19).要强调:利用对称性可以使计算量大大减少.
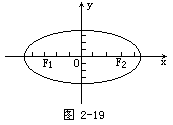

本例实质上是椭圆的第二定义,是为以后讲解抛物线和圆锥曲线的统一定义做准备的,同时再一次使学生熟悉求曲线方程的一般步骤,因此,要详细讲解:
设d是点M到直线l的距离,根据题意,所求轨迹就是集合P={M
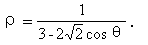
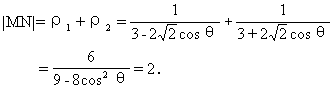
将上式化简,得:(a2-c2)x2+a2y2=a2(a2-c2).

这是椭圆的标准方程,所以点M的轨迹是椭圆.
由此例不难归纳出椭圆的第二定义.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com